
科目: 来源: 题型:
【题目】早在1960年、中国登山队首次从珠穆朗玛北侧中国境内登上珠峰,近几十年,珠峰更是吸引了大批的登山爱好者,某日,登山运动员傅博准备从海拔7400米的3号营地登至海拔近7900米的4号营地,由于天气骤变,近6小时的攀爬过程中他不得不几次下撤躲避强高空风,记向上爬升的海拔高度为正数,向下撒退时下降的海拔高度为负数,傅博在这一天攀爬的海拔高度记录如下:(单位:米)+320、-55、+116、-20、+81、-43、+115.
(1)傳博能按原计划在这天登至4号营地吗?
(2)若在这一登山过程中,傅博所处位置的海拔高度上升或下降1米平均消耗8大卡的卡路里,则傅博这天消耗了多少卡路里?
(3)登山消耗的卡路里预估为:1千克身体重量(体重或负重)1天需要55~65(大于等于55,小于等于65)大卡的卡路里,海拔6000米以上会使卡路里消耗增加20%,登山协会约定海拔5000米以上运动员负重14千克,在(2)的条件下,请你估算傳博的体重范围.(精确到1千克)
查看答案和解析>>
科目: 来源: 题型:
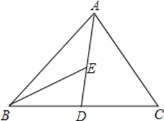
【题目】如图,AD为△ABC的中线,BE为三角形ABD中线,
(1)若∠ABE=20°,∠BAD=45°,求∠BED的度数;
(2)画出△BED中BD边上的高;
(3)若△ABC的面积为80,BD=8,则点E到BC边的距离为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B![]() C
C![]() D作匀速运动,那么△ABP的面积
D作匀速运动,那么△ABP的面积![]() 与点P运动的路程之间的函数图象大致是( ).
与点P运动的路程之间的函数图象大致是( ).

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源: 题型:
【题目】两组邻边分别相等的四边形我们称它为筝形,如图,在筝形ABCD中,AB=AD,BC=DC,AC,BD相交于点O.

(1)求证:①△ABC≌△ADC;②OB=OD,AC⊥BD;
(2)如果AC=6,BD=4,求筝形ABCD的面积.
查看答案和解析>>
科目: 来源: 题型:
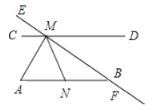
【题目】如图,∠CME+∠ABF=180°,MA平分∠CMN.若∠MNA=62°,求∠A的度数.根据提示将解题过程补充完整.
解:因为∠ABM+∠ABF=180°,
又因为∠CME+∠ABF=180°(已知),
所以∠ABM=∠CME
所以AB∥CD,理由:( )
所以∠CMN+( )=180°,
理由:(__________________________)
因为∠MNA=62°,
所以∠CMN=( )
因为MA平分∠CMN,
所以∠AMC=![]() ∠CMN =( ).(角平分线的定义)
∠CMN =( ).(角平分线的定义)
因为AB∥CD,
所以∠A=∠AMC=( )理由:(__________________________________)
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)在下列横线上用含有a,b的代数式表示相应图形的面积.
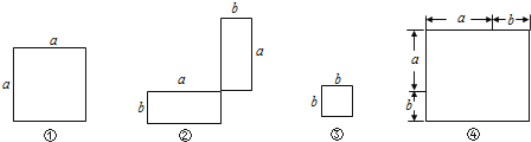
① ; ② ; ③ ; ④ .
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表示: ;
(3)利用(2)的结论计算992+2×99×1+1的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】(11分)如图,抛物线y=ax2+bx﹣3与x轴交于A,B两点,与y轴交于C点,且经过点(2,﹣3a),对称轴是直线x=1,顶点是M.
(1)求抛物线对应的函数表达式;
(2)经过C,M两点作直线与x轴交于点N,在抛物线上是否存在这样的点P,使以点P,A,C,N为顶点的四边形为平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)设直线y=﹣x+3与y轴的交点是D,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,试判断△AEF的形状,并说明理由;
(4)当E是直线y=﹣x+3上任意一点时,(3)中的结论是否成立(请直接写出结论).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com