
科目: 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 经过
经过![]() 两点,与x轴交于另一点B.点P是抛物线上的动点。
两点,与x轴交于另一点B.点P是抛物线上的动点。
(1)求抛物线的解析式;
(2)是否存在点P,使得△BCP是以BC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)当P运动到第一象限时,过P作直线PM平行y轴,交直线BC于点M。
①求线段PM长度的最大值
②D为平面内任意一点,当线段PM最大时,是否存在以C、P、M、D为顶点的平行四边形。若存在,直接写出所有符合条件的点D坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】提出问题:
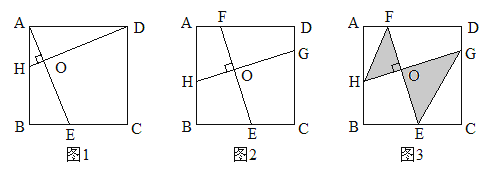
(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;
类比探究:
(2)如图2,在正方形ABCD中,点H,E,G,F分别在边AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由;
综合运用:
(3)在(2)问条件下,HF∥GE,如图3所示,已知BE=EC=2,EO=2FO,求图中阴影部分的面积。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,张明同学想测量某铜像的高度,已知铜像(图中![]() )高度比底座(图中
)高度比底座(图中![]() )高度多1米,张明随后用高度为1米的测角仪(图中
)高度多1米,张明随后用高度为1米的测角仪(图中![]() )测得铜像顶端点
)测得铜像顶端点![]() 的仰角β=51°24′,底座顶端点
的仰角β=51°24′,底座顶端点![]() 的仰角
的仰角![]() =26°36′.请你帮助张明算出铜像AB的高度(把铜像和底座近似看在一条直线上它的抽象几何图形如左图).(参考数据:sin26°36′≈0.45, cos26°36′≈0.89,tan26°36′≈0.5,sin51°24′≈0.78,cos51°24′≈0.6,tan51°24′≈1.25)
=26°36′.请你帮助张明算出铜像AB的高度(把铜像和底座近似看在一条直线上它的抽象几何图形如左图).(参考数据:sin26°36′≈0.45, cos26°36′≈0.89,tan26°36′≈0.5,sin51°24′≈0.78,cos51°24′≈0.6,tan51°24′≈1.25)

查看答案和解析>>
科目: 来源: 题型:
【题目】某中学为了丰富学生的校园体育锻炼生活,决定根据学生的兴趣爱好采购一批体育用品供学生课后锻炼使用,因此学校随机抽取了部分同学就兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:

(1)学校这次调查共抽取了 名学生;
(2)请补全条形统计图;
(3)在扇形统计图中,羽毛球部分所占的圆心角是 ;
(4)设该校共有学生1200名,请你估计该校有多少名学生喜欢跳绳?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B,如果△ABD的面积为15,那么△ACD的面积为( )

A. 15 B. 10 C. ![]() D. 5
D. 5
查看答案和解析>>
科目: 来源: 题型:
【题目】有![]() 筐白菜,以每筐
筐白菜,以每筐![]() 千克为标准,超过或不足的分别用正、负来表示,记录如下:
千克为标准,超过或不足的分别用正、负来表示,记录如下:
与标准质量的差 |
|
|
|
|
|
|
筐 数 |
|
|
|
|
|
|
(1)与标准质量比较,![]() 筐白菜总计超过或不足多少千克?
筐白菜总计超过或不足多少千克?
(2)若白菜每千克售价![]() 元,则出售这
元,则出售这![]() 筐白菜可卖多少元?
筐白菜可卖多少元?
查看答案和解析>>
科目: 来源: 题型:
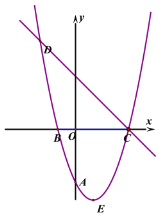
【题目】已知抛物线![]() 经过A(0,-3),B(-1,0),且抛物线对称轴为直线
经过A(0,-3),B(-1,0),且抛物线对称轴为直线![]() ,E
,E
是抛物线的顶点。
(1)求抛物线的解析式以及顶点坐标E。
(2)在![]() 轴上是否存在点P,使得
轴上是否存在点P,使得![]() 周长最短,若存在,请求出P点坐标,若不存在,请说
周长最短,若存在,请求出P点坐标,若不存在,请说
明理由。
(3)直线![]() 与抛物线交于C、D两点,Q是直线DC下方抛物线上的一点,是否存在点Q
与抛物线交于C、D两点,Q是直线DC下方抛物线上的一点,是否存在点Q
使得![]() 的面积最大,若存在请求出最大面积,若不存在,请说明理由。
的面积最大,若存在请求出最大面积,若不存在,请说明理由。
(4)抛物线上是否存在点M,使得![]() 是直角三角形,若存在,直接写出M点坐标,若不
是直角三角形,若存在,直接写出M点坐标,若不
存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com