
科目: 来源: 题型:
【题目】如图,在8×8的正方形网格中,△ABC的顶点和线段EF的端点都在小正方形的顶点上,这样的三角形叫做格点三角形.

(1)填空:∠ABC= ;
(2)请你在图中找出所有满足条件的点D(用黑圆点表示,标上D),使得以D、E、F为顶点的格点三角形与△ABC全等.
查看答案和解析>>
科目: 来源: 题型:
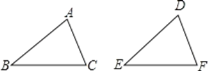
【题目】如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF; ②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=EF,∠C=∠F; ④AB=DE,AC=DF,∠B=∠E.能使△ABC≌△DEF有_____组.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学将组织七年级学生春游一天,由王老师和甲、乙两同学到客车租赁公司洽谈租车事宜.
(1)两同学向公司经理了解租车的价格,公司经理对他们说:“公司有45座和60座两种型号的客车可供租用,60座的客车每辆每天的租金比45座的贵100元.”王老师说:“我们学校八年级昨天在这个公司租了5辆45座和2辆60座的客车,一天的租金为1600元,你们能知道45座和60座的客车每辆每天的租金各是多少元吗”甲、乙两同学想了一下,都说知道了价格.
聪明的你知道45座和60座的客车每辆每天的租金各是多少元吗?
(2)公司经理问:“你们准备怎样租车”,甲同学说:“我的方案是只租用45座的客车,可是会有一辆客车空出30个座位”;乙同学说“我的方案只租用60座客车,正好坐满且比甲同学的方案少用两辆客车”,王老师在﹣旁听了他们的谈话说:“从经济角度考虑,还有别的方案吗”?如果是你,你该如何设计租车方案,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
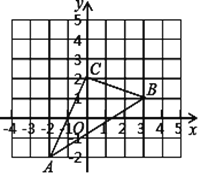
【题目】如图,△ABC在直角坐标系中,
(1)请写出![]() 各点的坐标;
各点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到![]() ,在图中画出三角形ABC变化后的位置,写出A′、B′、C′的坐标;
,在图中画出三角形ABC变化后的位置,写出A′、B′、C′的坐标;
(3)求出△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
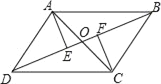
【题目】如图所示,已知AB∥CD,AD∥BC,AC与BD交于点O,AE⊥BD于E,CF⊥BD于E,图中全等三角形有( )
A. 3对 B. 5对 C. 6对 D. 7对
查看答案和解析>>
科目: 来源: 题型:
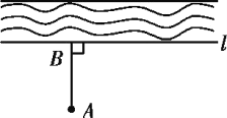
【题目】(1)如图,要把小河里的水引到田地A处,就作AB⊥l(垂足为B),沿AB挖水沟,水沟最短.理由是___________.
(2)把命题“平行于同一直线的两直线平行”写成“如果……,那么……”的形式._____________________________ .
(3)比较大小:![]() ______
______ ![]() .
.
(4)已知![]() 与
与![]() 是同类项,则m-3n的平方根是___.
是同类项,则m-3n的平方根是___.
(5)已知点P的坐标为(3a+6,2﹣a),且点P到两坐标轴的距离相等,则点P的坐标是______.
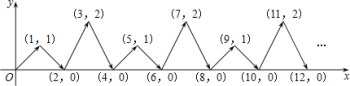
(6) 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2018次运动后,动点P的坐标是______________
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,等腰三角形ABC中,BD,CE分别是两腰上的中线.
(1)求证:BD=CE;
(2)设BD与CE相交于点O,点M,N分别为线段BO和CO的中点,当△ABC的重心到顶点A的距离与底边长相等时,判断四边形DEMN的形状,无需说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】图1是一个长为2m,宽为2n的长方形,将该长方形沿图中虚线用剪刀均分成四块小长方形,然后按照图2所示拼成一个正方形.
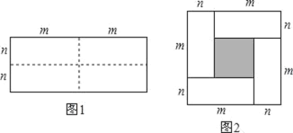
(1)使用不同方法计算图2中小正方形的面积,可推出(m+n)2,(m-n)2,mn之间的等量关系为: ;
(2)利用(1)中的结论,解决下列问题:
①已知a-b=4,ab=5,求a+b的值;
②已知a>0,a-![]() =2,求a+
=2,求a+![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题,请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长.

(1) 如图1,正方体的棱长为5cm一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处;
(2) 如图2,有一圆柱形食品盒,它的高等于16cm,底面直径为20cm.如果在盒外底面的边缘A处有一只蚂蚁,它想吃到盒外对面中点B处的食物;(盒的厚度和蚂蚁的大小忽略不计,结果可含π)
(3) 如图3, 有一无盖的圆柱形食品盒,它的高等于16cm,底面直径为20cm.如果在盒外底面的边缘A处有一只蚂蚁,它想吃到盒内对面中点B处的食物.(盒的厚度和蚂蚁的大小忽略不计,结果可含π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com