
科目: 来源: 题型:
【题目】计算张老师在黑板上写了三个算式,希望同学们认真观察,发现规律.

请你结合这些算式,解答下列问题:
(1)请你再写出另外两个符合上述规律的算式;
(2)验证规律:设两个连续奇数为2n+1,2n–1(其中n为正整数),则它们的平方差是8的倍数;
(3)拓展延伸:“两个连续偶数的平方差是8的倍数”,这个结论正确吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数轴上有两点A、B,点A表示的数是4,点B表示的数是﹣11,点C是数轴上一动点.
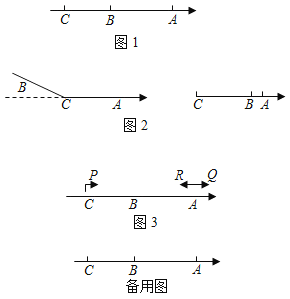
(1)如图1,若点C在点B的左侧,且BC:AB=3:5,求点C到原点的距离.
(2)如图2,若点C在A、B两点之间时,以点C为折点,将此数轴向右对折,当A、B两点之间的距离为1时,求C点在数轴上对应的数是多少?
(3)如图3,在(1)的条件下,动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度的2倍少5个单位长度/秒.经过4秒,点P、Q之间的距离是点Q、R之间距离的一半,求动点Q的速度.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年中国快递行业竞争激烈,为了占据市场赢得消费者青睐,某快递公司出台了市内快件收费标准:凡是重庆市内的快递统一收取基础费用8元,快递质量不超过10kg,不加收费用;快递质量大于10kg,则超过10g的部分按0.3元/kg收费.
(1)某同学需要将重量为x(x>10)千克的书籍在重庆市内同城快递回家,则该同学需付快递费用y元,用含x的代数式表示y.
(2)因国庆阅兵需要将一些纪念品从重庆寄往相距1800千米的北京,该快递公司获得这项任务后,调整了市外快件收费标准,收费标准如下表.已知纪念品重量为a千克,则纪念品从重庆运往北京的快递费为多少元?(用含a的代数式表示w)
价格表 | |
重量费 | 距离费 |
不超过10kg统一收取5元 | 0.01元/km |
超过10kg不超过50kg的部分0.2元/kg | |
超过50kg部分0.4元/kg | |
(注:快递费=重量费+距离费) | |
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示是一个正方体的表面展开图,请回答下列问题:

(1)与面B、面C相对的面分别是 和 ;
(2)若A=a3+![]() a2b+3,B=﹣
a2b+3,B=﹣![]() a2b+a3,C=a3﹣1,D=﹣
a2b+a3,C=a3﹣1,D=﹣![]() (a2b+15),且相对两个面所表示的代数式的和都相等,求E、F代表的代数式.
(a2b+15),且相对两个面所表示的代数式的和都相等,求E、F代表的代数式.
查看答案和解析>>
科目: 来源: 题型:
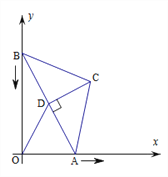
【题目】如图,在△ABC中,BC=AC=5,AB=8,CD为AB边的高,点A在x轴上,点B在y轴上,点C在第一象限,若A从原点出发,沿x轴向右以每秒1个单位长的速度运动,则点B随之沿y轴下滑,并带动△ABC在平面内滑动,设运动时间为t秒,当B到达原点时停止运动
(1)连接OC,线段OC的长随t的变化而变化,当OC最大时,t=____;
(2)当△ABC的边与坐标轴平行时,t=____。
查看答案和解析>>
科目: 来源: 题型:
【题目】在一个不透明的袋子里装有2个红球1个黄球,这3个小球除颜色不同外,其它都相同,贝贝同学摸出一个球后放回口袋再摸一个;莹莹同学一次摸2个球,两人分别记录下小球的颜色,关于两人摸到1个红球1个黄球和2个红球的概率的描述中,正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数轴上有两点A、B,点A表示的数是4,点B表示的数是﹣11,点C是数轴上一动点.

(1)如图1,若点C在点B的左侧,且BC:AB=3:5,求点C到原点的距离.
(2)如图2,若点C在A、B两点之间时,以点C为折点,将此数轴向右对折,当A、B两点之间的距离为1时,求C点在数轴上对应的数是多少?
(3)如图3,在(1)的条件下,动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度的2倍少5个单位长度/秒.经过4秒,点P、Q之间的距离是点Q、R之间距离的一半,求动点Q的速度.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com