
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,点E是BC延长线上的一点,且BD=DE.点G是线段BC的中点,连结AG,交BD于点F,过点D作DH⊥BC,垂足为H.
(1)求证:△DCE为等腰三角形;
(2)若∠CDE=22.5°,DC=![]() ,求GH的长;
,求GH的长;
(3)探究线段CE,GH的数量关系并用等式表示,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知Rt△ABC的斜边AB=6 cm,直角边AC=3 cm.
(1)以C为圆心,2 cm长为半径的圆和AB的位置关系是_________;
(2)以C为圆心,4 cm长为半径的圆和AB的位置关系是_________;
(3)如果以C为圆心的圆和AB相切,则半径长为_________。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某中学校园内有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,学校计划在中间留一块边长为(a+b)米的正方形地块修建一座雕像,然后将阴影部分进行绿化.

(1)求绿化的面积.(用含a、b的代数式表示)
(2)当a=2,b=4时,求绿化的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读理解:在平面直角坐标系中,若两点P、Q的坐标分别是P(x1,y1)、
Q(x2,y2),则P、Q这两点间的距离为|PQ|=![]() .如P(1,2),Q(3,4),则|PQ|=
.如P(1,2),Q(3,4),则|PQ|=![]() =2
=2![]() .
.
对于某种几何图形给出如下定义:符合一定条件的动点形成的图形,叫做符合这个条件的点的轨迹.如平面内到线段两个端点距离相等的点的轨迹是这条线段的垂直平分线.
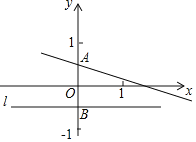
解决问题:如图,已知在平面直角坐标系xOy中,直线y=kx+![]() 交y轴于点A,点A关于x轴的对称点为点B,过点B作直线l平行于x轴.
交y轴于点A,点A关于x轴的对称点为点B,过点B作直线l平行于x轴.
(1)到点A的距离等于线段AB长度的点的轨迹是 ;
(2)若动点C(x,y)满足到直线l的距离等于线段CA的长度,求动点C轨迹的函数表达式;
问题拓展:(3)若(2)中的动点C的轨迹与直线y=kx+![]() 交于E、F两点,分别过E、F作直线l的垂线,垂足分别是M、N,求证:①EF是△AMN外接圆的切线;②
交于E、F两点,分别过E、F作直线l的垂线,垂足分别是M、N,求证:①EF是△AMN外接圆的切线;②![]() 为定值.
为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若矩形空地的面积为160m2,求x的值;
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
甲 | 乙 | 丙 | |
单价(元/棵) | 14 | 16 | 28 |
合理用地(m2/棵) | 0.4 | 1 | 0.4 |

查看答案和解析>>
科目: 来源: 题型:
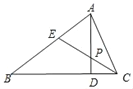
【题目】如图,在△ABC中,AD是△ABC的高线,CE是△ABC的角平分线,它们相交于点P.
(1)若∠B=40°,∠AEC=75°,求证:AB=BC;
(2)若∠BAC=90°,AP为△AEC边EC上中线,求∠B的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,AB=AC,P为斜边BC上一点(PB<CP),分别过点B,C作BE⊥AP于点E,CD⊥AP于点D.
(1)求证:AD=BE;
(2)若AE=2DE=2,求△ABC的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC和△ADE均为等边三角形,点O是AC的中点,点D在射线BO上,连结OE,EC,则∠ACE=_____°;若AB=1,则OE的最小值=_____.

查看答案和解析>>
科目: 来源: 题型:
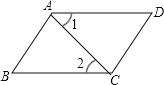
【题目】 根据题意,完成推理填空:如图,AB∥CD,∠1=∠2,试说明∠B=∠D.
解:∵∠1=∠2(已知)
∴ (內错角相等,两直线平行)
∴∠BAD+∠B=180°(两直线平行,同旁内角互补)
∵AB∥CD
∴ + =180°,
∴∠B=∠D
查看答案和解析>>
科目: 来源: 题型:
【题目】问题:已知α、β均为锐角,tanα=![]() ,tanβ=
,tanβ=![]() ,求α+β的度数.
,求α+β的度数.
探究:(1)用6个小正方形构造如图所示的网格图(每个小正方形的边长均为1),请借助这个网格图求出α+β的度数;
延伸:(2)设经过图中M、P、H三点的圆弧与AH交于R,求![]() 的弧长.
的弧长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com