科目： 来源：期末题 题型：填空题

观察下面一列数，按某种规律在横线上填上适当的数：…，则第n个数为(    )

科目： 来源：期末题 题型：解答题

探索n×n的正方形钉子板上（n是钉子板每边上的钉子数），连接任意两个钉子所得到的不同长度值的线段种数：
当n=2时，钉子板上所连不同线段的长度值只有1与，所以不同长度值的线段只有2种，若用S表示不同长度值的线段种数，则S=2；当n=3时，钉子板上所连不同线段的长度值只有1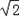，，2，，2五种，比n=2时增加了3种，即S=2+3=5．

（1）观察图形，填写下表：

（2）写出（n-1）×（n-1）和n×n的两个钉子板上，不同长度值的线段种数之间的关系；（用式子或语言表述均可）
（3）对n×n的钉子板，写出用n表示S的代数式

科目： 来源：河北省期中题 题型：解答题

科目： 来源：江西省模拟题 题型：填空题

科目： 来源：山东省中考真题 题型：填空题

数学的美无处不在，数学家们研究发现，弹拨琴弦发出声音的音调高低，取决于弦的长度，绷得一样紧的几根弦，如果长度的比能够表示成整数的比，发出的声音就比较和谐，例如，三根弦长度之比是15∶12∶10，把它们绷得一样紧，用同样的力弹拨，它们将分别发出很调和的乐声do、ｍi、so，研究15、12、10这三个数的倒数发现：，我们称15、12、10这三个数为一组调和数，现有一组调和数：x、5、3（x>5），则x的值是（    ）。

科目： 来源：期末题 题型：探究题

科目： 来源：河北省期末题 题型：填空题

科目： 来源：期末题 题型：填空题

科目： 来源：河北省期中题 题型：解答题

让我们轻松一下，做一个数字游戏：
第一步：取一个自然数n=5 ，计算n+1得a=（    ）；
第二步：算出a的各位数字之和得n，计算n+1得a=（    ）：
第三步：算出a的各位数字之和得n，再计算n＋1得a=（    ）；      
第四步：算出a的各位数字之和得n⁴，再计算n₄²＋1得a=（    ）…………，
则a₂₀₁₀=（    ）．

科目： 来源：期末题 题型：解答题