
科目: 来源:江西省模拟题 题型:解答题
查看答案和解析>>
科目: 来源:江苏省模拟题 题型:解答题

 ?
?查看答案和解析>>
科目: 来源:专项题 题型:解答题

查看答案和解析>>
科目: 来源:专项题 题型:解答题

查看答案和解析>>
科目: 来源:专项题 题型:解答题

查看答案和解析>>
科目: 来源:专项题 题型:解答题

查看答案和解析>>
科目: 来源:期中题 题型:解答题
| 某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表: | |||||||||
| |||||||||
| (1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并求出x的取值范围; (2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来; (3)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的A,B型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大? |
查看答案和解析>>
科目: 来源:上海期末题 题型:解答题
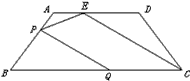
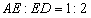 ,连结CE。点P是AB边上的一个动点,过点P作PQ⊥CE,交BC于点Q。设
,连结CE。点P是AB边上的一个动点,过点P作PQ⊥CE,交BC于点Q。设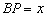 ,
,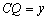 ,
,
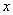 的值。
的值。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com