
科目: 来源:广东省中考真题 题型:解答题
| 如图,在Rt△ABC中,∠BAC=90°,∠C=60°,BC=24,点P是BC边上的动点(点P与点B、C不重合),过动点P作PD∥BA交AC于点D。 (1)若△ABC与△DPA相似,则∠APD是多少度? (2)试问:当PC等于多少时,△APD的面积最大?最大面积是多少? (3)若以线段AC为直径的圆和以线段BP为直径的圆相外切,求线段BP的长。 | |
 |
查看答案和解析>>
科目: 来源:广西自治区中考真题 题型:解答题
 △ABC中,AB=2,AC=BC= 5 .
△ABC中,AB=2,AC=BC= 5 .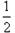 S△ABC;
S△ABC;
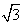 ,y4=-
,y4=-  .所以,原方程的解是y1=1,y2=-1,y3=
.所以,原方程的解是y1=1,y2=-1,y3= 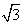 ,
, ,再如
,再如 ,可设
,可设 ,用同样的方法也可求解.
,用同样的方法也可求解.查看答案和解析>>
科目: 来源:上海期末题 题型:解答题
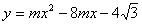 与
与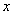 轴正半轴交于
轴正半轴交于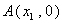 、
、 两点,且
两点,且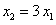 。
。
查看答案和解析>>
科目: 来源: 题型:
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为![]() 四等,并绘制成下面的频数分布表和扇形统计图.
四等,并绘制成下面的频数分布表和扇形统计图.
| 等第 | 成绩(得分) | 频数(人数) | 频率 |
| A | 10分 | 7 | 0.14 |
| 9分 | x | m | |
| B | 8分 | 15 | 0.30 |
| 7分 | 8 | 0.16 | |
| C | 6分 | 4 | 0.08 |
| 5分 | y | n | |
| D | 5分以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |

(1)试直接写出![]() 的值;
的值;
(2)求表示得分为![]() 等的扇形的圆心角的度数;
等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到![]() 等和
等和![]() 等的人数共有多少人?
等的人数共有多少人?
查看答案和解析>>
科目: 来源:李沧区一模 题型:解答题
查看答案和解析>>
科目: 来源:鼓楼区二模 题型:解答题
| 4 |
| 5 |
| x | 1 | 5 |
| y2 | 3.8 | 15 |
查看答案和解析>>
科目: 来源:不详 题型:解答题
| 周数x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 销售量y(件) | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
查看答案和解析>>
科目: 来源:西藏 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com