
科目: 来源:江苏中考真题 题型:解答题
 x与直线l2:y= -x+6相交于点M,直线l2与x轴相交于点N.
x与直线l2:y= -x+6相交于点M,直线l2与x轴相交于点N. C=2,边AB在x轴上,矩形ABCD沿x轴自左向右以每秒1个单位长度的速度移动,设矩形ABCD与△OMN的重叠部分的面积为S,移动的时间为t(从点B与点O重合时开始计时,到点A与点N重合时计时开始结束).直接写出S与自变量t之间的函数关系式(不需要给出解答过程).
C=2,边AB在x轴上,矩形ABCD沿x轴自左向右以每秒1个单位长度的速度移动,设矩形ABCD与△OMN的重叠部分的面积为S,移动的时间为t(从点B与点O重合时开始计时,到点A与点N重合时计时开始结束).直接写出S与自变量t之间的函数关系式(不需要给出解答过程).
查看答案和解析>>
科目: 来源:辽宁省中考真题 题型:解答题
 x2+mx+n的图象经过A,C两点.
x2+mx+n的图象经过A,C两点. OF为等腰三角形时,求此时点E的坐标;
OF为等腰三角形时,求此时点E的坐标; +1)倍.若存在,请直接写出点P的坐标;若不存在,请说明理由.
+1)倍.若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:新疆自治区中考真题 题型:解答题
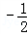 ,0),过A,C,D的抛物线与(1)所得的四边形OABC的边BC交于点E,求抛物线的解析式及点E的坐标;
,0),过A,C,D的抛物线与(1)所得的四边形OABC的边BC交于点E,求抛物线的解析式及点E的坐标;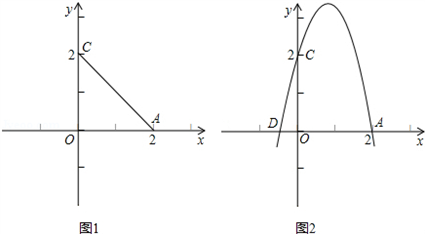
查看答案和解析>>
科目: 来源:四川省中考真题 题型:解答题
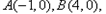 点C在y轴的正半轴上,且
点C在y轴的正半轴上,且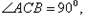 抛物线
抛物线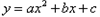 经过
经过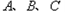 三点,其顶点为
三点,其顶点为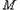 .
.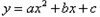 的解析式;
的解析式; 系,并加以证明;
系,并加以证明; ?如果存在,那么这样的点有几个?如果不存在,请说明理由。
?如果存在,那么这样的点有几个?如果不存在,请说明理由。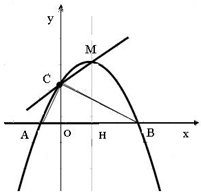
查看答案和解析>>
科目: 来源:山东省中考真题 题型:解答题

 约燃气10立方米,求该家庭以前每月的平均燃气用量.
约燃气10立方米,求该家庭以前每月的平均燃气用量.
查看答案和解析>>
科目: 来源:黑龙江省中考真题 题型:解答题
 x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3. 若点D(2,2)是抛物线上一点,那么在
若点D(2,2)是抛物线上一点,那么在 抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小,若存在,请求出点P的坐标,若不存在,请说明理由.
抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小,若存在,请求出点P的坐标,若不存在,请说明理由. 

查看答案和解析>>
科目: 来源:山东省中考真题 题型:解答题
 交于M、N两点.分别过点C,D(0,﹣2)作平行于x轴的直线l1、l2.
交于M、N两点.分别过点C,D(0,﹣2)作平行于x轴的直线l1、l2.
查看答案和解析>>
科目: 来源:福建省中考真题 题型:解答题

查看答案和解析>>
科目: 来源:山东省中考真题 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com