
科目: 来源:山东省中考真题 题型:解答题
查看答案和解析>>
科目: 来源:山东省中考真题 题型:单选题
查看答案和解析>>
科目: 来源:山东省中考真题 题型:解答题

查看答案和解析>>
科目: 来源:山东省中考真题 题型:解答题
如图,半径为2的⊙C与x轴的正半轴交于点A,与y轴的正半轴交于点B,点C的坐标为
(1,0).若抛物线y=﹣ x2+bx+c过A、B两点.
x2+bx+c过A、B两点.
(1)求抛物线的解析式;
(2)在抛物线上是否存在点P,使得∠PBO=∠POB?若存在,求出点P的坐标;若不存在说明理由;
(3)若点M是抛物线(在第一象限内的部分)上一点,△MAB的面积为S,求S的最大(小)值.

查看答案和解析>>
科目: 来源:上海中考真题 题型:解答题
 ,EF⊥OD,垂足为F.
,EF⊥OD,垂足为F.
查看答案和解析>>
科目: 来源:四川省中考真题 题型:解答题
 ,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2.
,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2. ?若存在,求出点Q的坐标;若不存在,请说明理由.
?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:山东省中考真题 题型:解答题

查看答案和解析>>
科目: 来源:四川省中考真题 题型:操作题
 可以设矩形的一边长为x,面积为s,则s与x的函数关系式为:
可以设矩形的一边长为x,面积为s,则s与x的函数关系式为: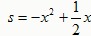 (x﹥0),利用函数的图象或通过配方均可求得该函数的最大值。
(x﹥0),利用函数的图象或通过配方均可求得该函数的最大值。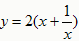 (x﹥0),问题就转化为研究该函数的最大(小)值了。
(x﹥0),问题就转化为研究该函数的最大(小)值了。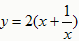 (x﹥0)的最大(小)值。
(x﹥0)的最大(小)值。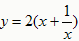 (x﹥0)的图象:
(x﹥0)的图象: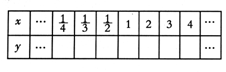
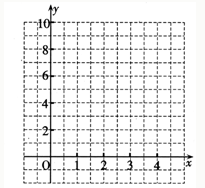
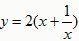 (x﹥0)
(x﹥0) 有最 (填“大”或“小”)是 。
有最 (填“大”或“小”)是 。 证:问题背景中提到,通过配方可求二次函数
证:问题背景中提到,通过配方可求二次函数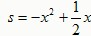 (x﹥0)的最大值,请你尝试通过配方求函数
(x﹥0)的最大值,请你尝试通过配方求函数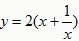 (x﹥0)的最大(小)值,以证明你的猜想。〔提示:当x>0时,x=
(x﹥0)的最大(小)值,以证明你的猜想。〔提示:当x>0时,x=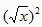 〕
〕查看答案和解析>>
科目: 来源:四川省中考真题 题型:解答题
 .
.
查看答案和解析>>
科目: 来源:甘肃省中考真题 题型:解答题
 x2+bx+c经过点B,且顶点在直线x=
x2+bx+c经过点B,且顶点在直线x= 上.
上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com