
科目: 来源:河北省同步题 题型:填空题

查看答案和解析>>
科目: 来源:河北省同步题 题型:填空题

查看答案和解析>>
科目: 来源:河北省同步题 题型:解答题
 的图象经过(2)中抛物线上的点(1,a),试在图(2)所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较y1与y2的大小。
的图象经过(2)中抛物线上的点(1,a),试在图(2)所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较y1与y2的大小。
查看答案和解析>>
科目: 来源:河北省同步题 题型:解答题
查看答案和解析>>
科目: 来源:湖北省模拟题 题型:解答题
 x+1 。
x+1 。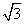 个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒。
个单位长度的速度向点O移动,动点Q从点O开始在线段OA上以每秒1个单位长度的速度向点A移动,(P、Q两点同时开始移动)设P、Q移动的时间为t秒。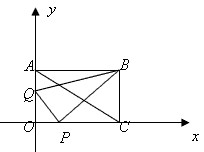
查看答案和解析>>
科目: 来源:北京期中题 题型:解答题

查看答案和解析>>
科目: 来源:湖南省中考真题 题型:解答题
 x2+1,直线y=kx+b经过点B(0,2)。
x2+1,直线y=kx+b经过点B(0,2)。
 x2+1相交,其中一个交点为P,求出P的坐标;
x2+1相交,其中一个交点为P,求出P的坐标; x2+1相交,其中一个交点为P'(如图②),过点P'作x轴的垂线P'M,点M为垂足,是否存在这样的点P',使△P'BM为等边三角形?若存在,请求出点P'的坐标;若不存在,请说明理由。
x2+1相交,其中一个交点为P'(如图②),过点P'作x轴的垂线P'M,点M为垂足,是否存在这样的点P',使△P'BM为等边三角形?若存在,请求出点P'的坐标;若不存在,请说明理由。查看答案和解析>>
科目: 来源:河北省同步题 题型:单选题

[ ]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com