
科目: 来源:期中题 题型:解答题
 与x轴和y轴交于点A、C两点,抛物线
与x轴和y轴交于点A、C两点,抛物线 经过点A、C,点B是抛物线与x轴的另一个交点.
经过点A、C,点B是抛物线与x轴的另一个交点. 与(1)中所求的抛物线交于M、N两点,问:是否存在a的值,使得∠MON=90°,若存在,求出a的值,若不存在,请说明理由。
与(1)中所求的抛物线交于M、N两点,问:是否存在a的值,使得∠MON=90°,若存在,求出a的值,若不存在,请说明理由。 
查看答案和解析>>
科目: 来源:四川省中考真题 题型:解答题
 与x轴交于A、B两点,与y轴交于点C(0,-1),且对称轴x=1。
与x轴交于A、B两点,与y轴交于点C(0,-1),且对称轴x=1。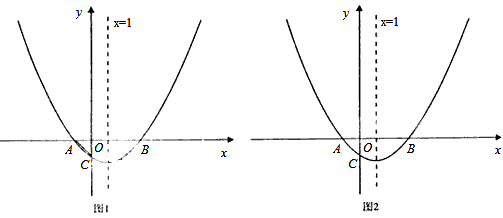
查看答案和解析>>
科目: 来源:河南省同步题 题型:单选题
查看答案和解析>>
科目: 来源:北京期末题 题型:单选题
 x2先向左平移2个单位,再向下平移1个单位得到新的抛物线,则新抛物线的解析式是
x2先向左平移2个单位,再向下平移1个单位得到新的抛物线,则新抛物线的解析式是  (x+2)2-1
(x+2)2-1 (x-2)2-1
(x-2)2-1查看答案和解析>>
科目: 来源:贵州省中考真题 题型:解答题

查看答案和解析>>
科目: 来源:贵州省中考真题 题型:解答题

查看答案和解析>>
科目: 来源:河南省中考真题 题型:解答题

查看答案和解析>>
科目: 来源:湖北省中考真题 题型:解答题
 ),∠BCO= 60°,OH⊥BC于点H。动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,设点P运动的时间为t秒。
),∠BCO= 60°,OH⊥BC于点H。动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,设点P运动的时间为t秒。 
查看答案和解析>>
科目: 来源:安徽省中考真题 题型:解答题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com