
科目: 来源:专项题 题型:解答题
 米,入水距池边的距离为4米,同时,运动员在距水面高度为5米以前,必须完成规定的翻腾动作,并调整好人水姿势,否则就会出现失误。
米,入水距池边的距离为4米,同时,运动员在距水面高度为5米以前,必须完成规定的翻腾动作,并调整好人水姿势,否则就会出现失误。 
 米,问此次跳水会不会失误?并通过计算说明理由。
米,问此次跳水会不会失误?并通过计算说明理由。查看答案和解析>>
科目: 来源:专项题 题型:解答题

查看答案和解析>>
科目: 来源:专项题 题型:解答题

查看答案和解析>>
科目: 来源:专项题 题型:单选题
查看答案和解析>>
科目: 来源:专项题 题型:解答题
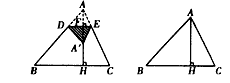
查看答案和解析>>
科目: 来源:期中题 题型:解答题

查看答案和解析>>
科目: 来源:专项题 题型:解答题
查看答案和解析>>
科目: 来源:专项题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com