科目： 来源：江苏期中题 题型：解答题

抛物线y=ax²+2x+3（a＜0）交X轴于A，B两点，交Y轴于点C，顶点为D，而且经过点（2，3）。
（1）写出抛物线的解析式及C、D两点的坐标；
（2）连结BC，以BC为边向右作正方形BCEF，求E、F两点的坐标；
（3）若将此抛物线沿其对称轴向上平移，试判断平移后的抛物线是否会同时经过正方形BCEF的两个顶点E、F；若能，写出平移后的抛物线解析式，若不能，请说明理由。

科目： 来源：江苏期中题 题型：解答题

已知抛物线经过点A（5，0）、B（6，-6）和原点.

（1）求抛物线的函数关系式；
（2）若过点B的直线y=kx+b'与抛物线相交于点C（2，m），请求出△OBC的面积S的值.
（3）过点C作平行于x轴的直线交y轴于点D，在抛物线对称轴右侧位于直线DC下方的抛物线上任取一点P，过点P作直线PF平行于y轴交x轴于点F，交直线DC于点E. 直线PF与直线DC及两坐标轴围成矩形OFED（如图），是否存在点P，使得△OCD与△CPE相似？若存在，求出点P的坐标；若不存在，请说明理由.

科目： 来源：江苏期中题 题型：解答题

如图，以矩形OABC的两边OA和OC所在直线为x轴、y轴建立平面直角坐标系，A点的坐标为（3，0），C点的坐标为（0，4）。将矩形OABC绕O点逆时针旋转，使B点落在y轴的正半轴上，旋转后的矩形为OA₁B₁C₁，BC，A₁B₁相交于点M。
（1）求点B₁的坐标与线段B₁C的长；
（2）将图a中的矩形OA₁B₁C₁沿y轴向上平移，如图b，矩形PA₂B₂C₂是平移过程中的某一位置，BC、A₂B₂相交 于点M₁，点P运动到C点停止。设点P运动的距离x，矩形PA₂B₂C₂与原矩形OABC重叠部分的面积为y，求y关于x的函数关系式，并写出x的取值范围；
（3）如图c，当点P运动到点C时，平移后的矩形为PA₃B₃C₃，请你思考如何通过图形变换使矩形PA₃B₃C₃与原矩形OABC重合，请简述你的做法。

科目： 来源：期中题 题型：解答题

科目： 来源：安徽省期中题 题型：解答题

如图，在平面直角坐标系中，两个一次函数y=x，y=-2x+12的图象相交于点A，动点E从O点出发，沿OA方向以每秒1个单位的速度运动，作EF∥y轴与直线BC交于点F，以EF为一边向x轴负方向作正方形EFMN，设正方形EFMN与△AOC的重叠部分的面积为S.

（1）求点A的坐标；
（2）求过A、B、O三点的抛物线的顶点P的坐标；
（3）当点E在线段OA上运动时，求出S与运动时间t（秒）的函数表达式；
（4）在（3）的条件下，t为何值时，S有最大值，最大值是多少？此时（2）中的抛物线的顶点P是否在直线EF上，请说明理由.

科目： 来源：同步题 题型：单选题

设y=y₁+y₂，且y₁与x²成正比例，y₂与成反比例，则y与x的函数关系是

[     ]

A.正比例函数
B.一次函数
C.二次函数
D.反比例函数

科目： 来源：专项题 题型：解答题

已知：在△ABC中，，P为AB上一动点（P不与A、B重合），过点P作PE//BC交AC于E，连结BE，设AP=x，△BPE的面积为y，求y与x之间的函数关系，并求自变量x的取值范围。

科目： 来源：模拟题 题型：解答题

有一座大桥是靠抛物线型的拱形支撑的，它的桥面处于拱形中部（金华市区的双龙大桥就是这种模型）已知桥面在拱形之间的宽度为40m，桥面离拱形支撑的最高点O的距离为10m，且在正常水位时水面宽度AB为48m
（1）建立如图所示的直角坐标系，求此抛物线的解析式；
（2）现有一辆载有救援物质的货车正以40的速度必需经过此桥匀速开往乙地，当货车行驶到甲地时接到紧急通知：前方连降暴雨，造成水位以每小时0.3m的速度持续上涨（接到通知时水位已经比正常水位高出2m了，当水位到达桥面的高度时，禁止车辆通行），已知甲地距离此桥360km（桥长忽略不计），请问：如果货车按原来速度行驶，能否安全通过此桥？若能，请说明理由；若不能，要使货车安全通过此桥，速度不得低于多少？

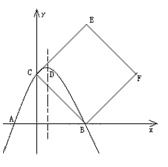
科目： 来源：模拟题 题型：解答题

如图，矩形是由矩形（边OA在x轴正半轴上，边OC在y轴正半轴上）绕点B逆时针旋转得到的，点在x轴的正半轴上，B点的坐标为 （1，3），与AB交于D点。

（1）求D点的坐标；
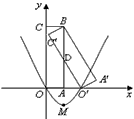
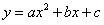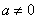（2）如果二次函数（）的图象经过点O、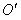两点且图象顶点M的纵坐标为-1，求这个二次函数的解析式；
（3）若将直线OC绕点O旋转度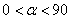（）后与抛物线的另一个交点为P，则以O、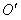、B、P为顶点的四边形能否是平行四边形？若能，求出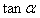的值；若不能，请说明理由。

科目： 来源：江苏模拟题 题型：解答题

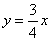矩形OABC在直角坐标系中的位置如图所示，A、C两点的坐标分别为A（6，0）、C（0，3），直线与BC边相交于点D。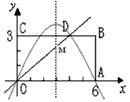

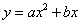（1）求点D的坐标；
（2）若抛物线经过D、A两点，试确定此抛物线的函数表达式；
（3）若P为x轴上方（2）中抛物线上一点，求△POA面积的最大值；
（4）设（2）中抛物线的对称轴与直线OD交于点M，点Q为对称轴上一动点，以Q、O、M为顶点的三角形与△OCD相似，求符合条件的Q点的坐标。