
科目: 来源:重庆市期末题 题型:解答题
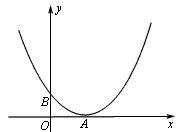
已知抛物线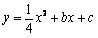 过点(-2,4),与y轴的交点为B(0,1)。 过点(-2,4),与y轴的交点为B(0,1)。(1)求抛物线的解析式及其顶点A的坐标; (2)在抛物线上是否存在一点C,使∠BAC=90。?若不存在说明理由;若存在,求出点C的坐标; (3)P、Q为抛物线上的两点,且横坐标分别为4和6,在x轴、y轴上分别有两个动点M、N,当PM +MN +NQ最小时,求出M、N两点的坐标。 |
 |
查看答案和解析>>
科目: 来源:北京期末题 题型:解答题
 的部分对应值如下表:
的部分对应值如下表: 
查看答案和解析>>
科目: 来源:北京期末题 题型:解答题

查看答案和解析>>
科目: 来源:北京期末题 题型:解答题
 交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的横坐标是-3,点B的横坐标是1。
交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的横坐标是-3,点B的横坐标是1。 ,
, ,
,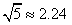 )
) 
查看答案和解析>>
科目: 来源:重庆市期末题 题型:解答题
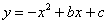
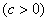 的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M。
的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M。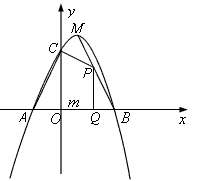
查看答案和解析>>
科目: 来源:广西自治区中考真题 题型:解答题
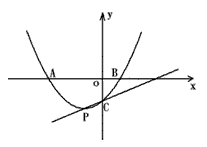
| 已知抛物线y=x2+bx+c的图象过A(0,1)、B(-1,0)两点,直线l:x=-2与抛物线相交于点C,抛物线上一点M从B点出发,沿抛物线向左侧运动,直线MA分别交对称轴和直线l于D、P两点,设直线PA为y=kx+m,用S表示以P、B、C、D为顶点的多边形的面积。 |
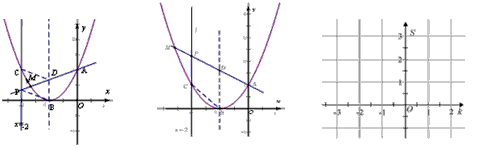 |
| (1)求抛物线的解析式,并用k表示P、D两点的坐标; (2)当0<k≤1时,求S与k之间的关系式; (3)当k<0时,求S与k之间的关系式,是否存在k的值,使得以P、B、C、D为顶点的多边形为平行四边形,若存在,求此时的值.若不存在,请说明理由; (4)若规定k=0时,y=m是一条过点(0,m)且平行于x轴的直线.当k≤1时,请在下面给出的直角坐标系中画出S与k之间的函数图象,求S的最小值,并说明此时对应的以P、B、C、D为顶点的多边形的形状。 |
查看答案和解析>>
科目: 来源:福建省模拟题 题型:解答题
| 宏达纺织品有限公司准备投资开发A、B两种新产品,通过市场调研发现:如果单独投资A种产品,则所获利润yA(万元)与投资金额x(万元)之间满足正比例函数关系:yA=kx;如果单独投资B种产品,则所获利润yB(万元)与投资金额x(万元)之间满足二次函数关系:yB=ax2+bx.根据公司信息部的报告,yA,yB(万元)与投资金额x(万元)的部分对应值(如下表) | |||||||||
| |||||||||
| (1)求yA,yB的解析式; (2)如果公司准备投资20万元同时开发A、B两种新产品,设公司所获得的总利润为w(万元),试写出w与某种产品的投资金额x之间的函数关系式; (3)请你设计一个在(2)中能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少万元? |
查看答案和解析>>
科目: 来源:福建省模拟题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com