
科目: 来源:浙江省中考真题 题型:解答题

查看答案和解析>>
科目: 来源:浙江省中考真题 题型:解答题

 、2
、2 ;
;查看答案和解析>>
科目: 来源:江苏期中题 题型:解答题
 、
、 、
、 ,求这个三角形的面积。小华同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示,这样就不需要求△ABC的高,而借用网格就能计算出它的面积。
,求这个三角形的面积。小华同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示,这样就不需要求△ABC的高,而借用网格就能计算出它的面积。
 、
、 、
、 (x>0),请利用图②的正方形网格(每个小正方形的边长为)画出相应的△ABC,并求出它的面积。
(x>0),请利用图②的正方形网格(每个小正方形的边长为)画出相应的△ABC,并求出它的面积。 、
、 、
、 (a>0,b>0,且a≠b),试运用构图法求出这个三角形的面积。
(a>0,b>0,且a≠b),试运用构图法求出这个三角形的面积。查看答案和解析>>
科目: 来源:期末题 题型:解答题
查看答案和解析>>
科目: 来源:同步题 题型:单选题
A.
B.
C.
D.
查看答案和解析>>
科目: 来源:期末题 题型:解答题
如图,△AOB是含45°角的直角三角尺,即OA=OB,且S△AOB=2。
(1)求A、B两点的坐标;
(2)M是AB的中点,C是x轴负半轴上的一点,问:是否存在点C,使得S△ACM=S△OAB?若存在,求出C 点的坐标;若不存在,请说明理由;
(3)在(2)的条件下,设P是OC上的动点,过P作PD⊥AB于D,交y轴于Q,当P在OC上运动时,下列两个结论:①∠PQB+∠OAB的值不变;②S△POQ+S△BDQ的值不变,只有一个正确,请判断出正确结论并求其值。

查看答案和解析>>
科目: 来源:专项题 题型:填空题

查看答案和解析>>
科目: 来源:同步题 题型:解答题
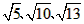 ,求这个三角形的面积。
,求这个三角形的面积。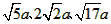 (a>0),请利用图(2)的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积;
(a>0),请利用图(2)的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积;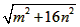 、
、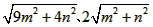 (m>0,n>0,且m≠n),试运用构图法求出这个三角形的面积。
(m>0,n>0,且m≠n),试运用构图法求出这个三角形的面积。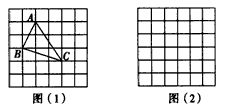
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com