问题提出：以n边形的n个顶点和它内部的m个点，共（m+n）个点作为顶点，可把原n边形分割成多少个互不重叠的小三角形？问题探究：为了解决上面的问题，我们将采取一般问题特殊性的策略，先从简单和具体的情形入手：
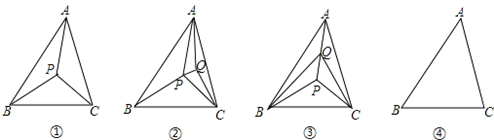
探究一：以△ABC的三个顶点和它内部的1个点P，共4个点为顶点，可把△ABC分割成多少个互不重叠的小三角形？如图①，显然，此时可把△ABC分割成3个互不重叠的小三角形．探究二：以△ABC的三个顶点和它内部的2个点P、Q，共5个点为顶点，可把△ABC分割成多少个互不重叠的小三角形？在探究一的基础上，我们可看作在图①△ABC的内部，再添加1个点Q，那么点Q的位置会有两种情况：一种情况，点Q在图①分割成的某个小三角形内部．不妨假设点Q在△PAC内部，如图②；另一种情况，点Q在图①分割成的小三角形的某条公共边上．不妨假设点Q在PA上，如图③．显然，不管哪种情况，都可把△ABC分割成5个不重叠的小三角形．
探究三：以△ABC的三个顶点和它内部的3个点P、Q、R，共6个点为顶点可把△ABC分割成 （ ）个互不重叠的小三角形，并在图④中画出一种分割示意图．
探究四：以△ABC的三个顶点和它内部的m个点，共（m+3）个顶点可把△ABC分割成（ ）个互不重叠的小三角形．
探究拓展：以四边形的4个顶点和它内部的m个点，共（m+4）个顶点可把四边形分割成（ ）个互不重叠的小三角形．
问题解决：以n边形的n个顶点和它内部的m个点，共（m+n）个顶点可把△ABC分割成（ ）个互不重叠的小三角形．
实际应用：以八边形的8个顶点和它内部的2012个点，共2020个顶点，可把八边形分割成多少个互不重叠的小三角形？（要求列式计算）
的等腰三角形纸片，现过底边上一点，沿与底边垂直的方向将其剪开，分成三角形和四边形两部分，则四边形中，最大角的度数是（ ）.
