
科目: 来源: 题型:
 4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.
4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.查看答案和解析>>
科目: 来源: 题型:
 3、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.
3、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.查看答案和解析>>
科目: 来源: 题型:
| A、300名学生的身高是总体 | B、这300名学生的平均身高估计是163(cm) | C、这10名学生身高的众数和中位数是165(cm) | D、这10名学生的身高是样本容量 |
查看答案和解析>>
科目: 来源: 题型:
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| a |
| 1 |
| b |
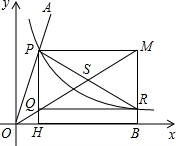 ∠MOB=
∠MOB=| 1 |
| 3 |
查看答案和解析>>
科目: 来源: 题型:
| 三边a、b、c | a+b-c |
| ||
| 6,8,10 | 4 | 1 | ||
| 8,15,17 | 6 |
| ||
| 9,40,41 | 8 | 2 |
| S |
| L |
查看答案和解析>>
科目: 来源: 题型:
| k | x |
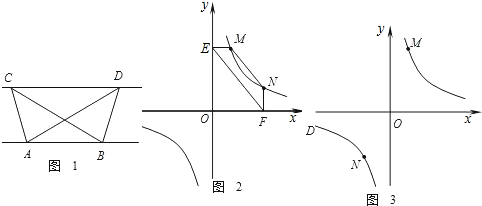
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com