
科目: 来源: 题型:
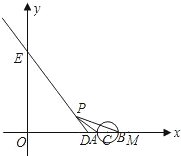 以1个单位长度/秒的速度沿射线DE的方向作匀速运动.设运动时间为t秒.
以1个单位长度/秒的速度沿射线DE的方向作匀速运动.设运动时间为t秒.| 1 | 2 |
查看答案和解析>>
科目: 来源: 题型:
 已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(2,0),C(0,-2),直线x=m(m>2)与x轴交于点D.
已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(2,0),C(0,-2),直线x=m(m>2)与x轴交于点D.查看答案和解析>>
科目: 来源: 题型:
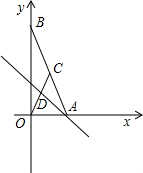 18x+72=0的两个根,点C是线段AB的中点,点D在线段OC上,OD=2CD.
18x+72=0的两个根,点C是线段AB的中点,点D在线段OC上,OD=2CD.查看答案和解析>>
科目: 来源: 题型:
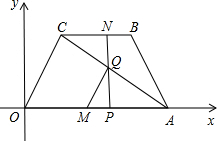 度向终点C运动(M到达点A后停止,点N继续运动到C点停止),过点N作NP⊥OA于P点,连接AC交NP于Q,连接MQ,如动点N运动时间为t秒.
度向终点C运动(M到达点A后停止,点N继续运动到C点停止),过点N作NP⊥OA于P点,连接AC交NP于Q,连接MQ,如动点N运动时间为t秒.查看答案和解析>>
科目: 来源: 题型:
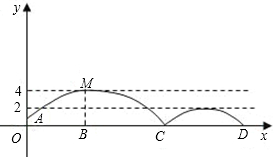 弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.| 3 |
| 6 |
查看答案和解析>>
科目: 来源: 题型:
| PQ |
| PC |
| AD |
| AB |
| 3 |
| 2 |
| S△APQ |
| S△PBC |
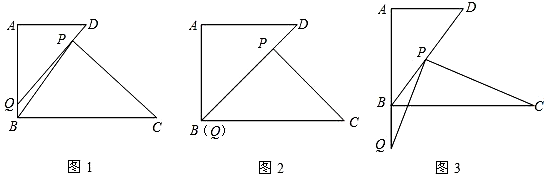
查看答案和解析>>
科目: 来源: 题型:
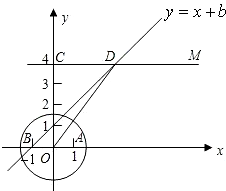 直线CM∥x轴(如图所示).点B与点A关于原点对称,直线y=x+b(b为常数)经过点B,且与直线CM相交于点D,连接OD.
直线CM∥x轴(如图所示).点B与点A关于原点对称,直线y=x+b(b为常数)经过点B,且与直线CM相交于点D,连接OD.查看答案和解析>>
科目: 来源: 题型:
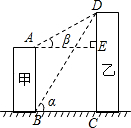 从A点测得D点的仰角β为30°,已知甲建筑物高AB=36米.
从A点测得D点的仰角β为30°,已知甲建筑物高AB=36米.| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com