
科目: 来源: 题型:
|
|
查看答案和解析>>
科目: 来源: 题型:
 33、如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
33、如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:查看答案和解析>>
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
 某同学用牙膏纸盒制作一个如图所示的笔筒,笔筒的筒底为长4.5厘米,宽3.4厘米的矩形.则该笔筒最多能放半径为0.4厘米的圆柱形铅笔( )
某同学用牙膏纸盒制作一个如图所示的笔筒,笔筒的筒底为长4.5厘米,宽3.4厘米的矩形.则该笔筒最多能放半径为0.4厘米的圆柱形铅笔( )| A、20支 | B、21支 | C、22支 | D、25支 |
查看答案和解析>>
科目: 来源: 题型:
| 14 |
| 6 |
| 14+6 |
| 14 |
| 9 |
| 6 |
| 4 |
| 14 |
| 6 |
| 14+6 |
| 20 |
| 25 |
| 14 |
| 6 |
| 14+6 |
| 14 |
| 6 |
| 14 |
| 6 |
| 14+6 |
| A、两人都正确 |
| B、两人都错误 |
| C、甲正确,乙错误 |
| D、甲错误,乙正确 |
查看答案和解析>>
科目: 来源: 题型:
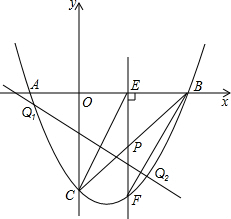 x轴于E,交抛物线于F.
x轴于E,交抛物线于F.查看答案和解析>>
科目: 来源: 题型:

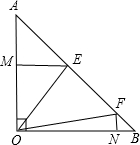
 如图1是脚踩式家用垃圾桶,图2是它的内部结构示意图.EF是一根固定的圆管,轴MN两头是可以滑动的圆珠,且始终在圆管内上下滑动.点A是横杆BN转动的支点.当横杆BG踩下时,N移动到N′.已知点B、A、N、G的水平距离如图所示,支点的高度为3cm.
如图1是脚踩式家用垃圾桶,图2是它的内部结构示意图.EF是一根固定的圆管,轴MN两头是可以滑动的圆珠,且始终在圆管内上下滑动.点A是横杆BN转动的支点.当横杆BG踩下时,N移动到N′.已知点B、A、N、G的水平距离如图所示,支点的高度为3cm.查看答案和解析>>
科目: 来源: 题型:
 如图,已知等腰Rt△AOB,其中∠AOB=90°,OA=OB=2,E、F为斜边AB上的两个动点(E比F更靠近A),满足∠EOF=45°,
如图,已知等腰Rt△AOB,其中∠AOB=90°,OA=OB=2,E、F为斜边AB上的两个动点(E比F更靠近A),满足∠EOF=45°,| x |
| y |
| xy |
| 1 |
| x |
| x |
| 1 | ||
|
查看答案和解析>>
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
| 销售单价x(元/件) | … | 30 | 40 | 50 | 60 | … |
| 每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
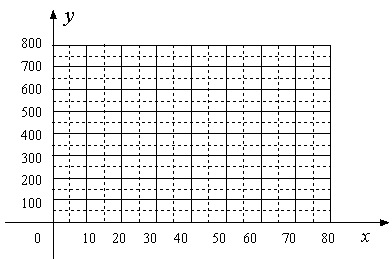
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com