
科目: 来源: 题型:
 过点E作⊙O的切线分别交AC,BD于点C,D,连接OC,OD分别交AE,BE于点M,N.
过点E作⊙O的切线分别交AC,BD于点C,D,连接OC,OD分别交AE,BE于点M,N.查看答案和解析>>
科目: 来源: 题型:
 2005年10月,继杨利伟之后,航天员费俊龙、聂海胜又遨游了太空,这大大激发了王红庭同学爱好天文学的热情.他通过上网查阅资料了解到,金星和地球的运行轨道可以近似地看作是以太阳为圆心的同心圆,且这两个同心圆在同一平面上(如图所示),由于金星和地球的运转速度不同,所以两者的位置不断发生变化,当金星、地球距离最近试,此时叫“下合”;当金星、地球距离最远时,此时叫“上合”;在地球上观察金星的视线恰好与金星轨道相切时,此时分别叫“东大距”和“西大距”,已知地球与太阳相距约为15(千万km),金星与太阳相距约10(千万km),分别求“下合”、“东大距”、“西大距”、“上合”时,金星、地球的距离(可用根号表示).
2005年10月,继杨利伟之后,航天员费俊龙、聂海胜又遨游了太空,这大大激发了王红庭同学爱好天文学的热情.他通过上网查阅资料了解到,金星和地球的运行轨道可以近似地看作是以太阳为圆心的同心圆,且这两个同心圆在同一平面上(如图所示),由于金星和地球的运转速度不同,所以两者的位置不断发生变化,当金星、地球距离最近试,此时叫“下合”;当金星、地球距离最远时,此时叫“上合”;在地球上观察金星的视线恰好与金星轨道相切时,此时分别叫“东大距”和“西大距”,已知地球与太阳相距约为15(千万km),金星与太阳相距约10(千万km),分别求“下合”、“东大距”、“西大距”、“上合”时,金星、地球的距离(可用根号表示).查看答案和解析>>
科目: 来源: 题型:
 件表示r.
件表示r.查看答案和解析>>
科目: 来源: 题型:
 ABC=30°.
ABC=30°.查看答案和解析>>
科目: 来源: 题型:
 已知,在△ABC中(∠A<∠B),AB=AC=8,cosA=
已知,在△ABC中(∠A<∠B),AB=AC=8,cosA=| 7 | 8 |
查看答案和解析>>
科目: 来源: 题型:
 抛物线y=ax2+bx+c的图象如图所示,已知该抛物线与x轴交于A、B两点,顶点为C,
抛物线y=ax2+bx+c的图象如图所示,已知该抛物线与x轴交于A、B两点,顶点为C,查看答案和解析>>
科目: 来源: 题型:
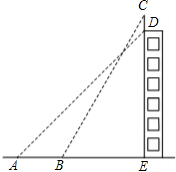 如图,某幢大楼顶部有一块3米高的广告牌CD,小明在A点测得点D的仰角是45°,走近9米在B点测得点C的仰角是60°,且A、B、E三点在一条直线上.求这幢大楼DE的高度(
如图,某幢大楼顶部有一块3米高的广告牌CD,小明在A点测得点D的仰角是45°,走近9米在B点测得点C的仰角是60°,且A、B、E三点在一条直线上.求这幢大楼DE的高度(| 3 |
查看答案和解析>>
科目: 来源: 题型:
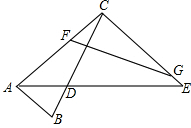 点E.
点E.| FC |
| CG |
| AD |
| ED |
查看答案和解析>>
科目: 来源: 题型:
 如图,已知在△ABC中,∠C=90°,点D在BC上,∠B=∠DAC,且S△ACD:S△BCA=4:9,若AC=6.
如图,已知在△ABC中,∠C=90°,点D在BC上,∠B=∠DAC,且S△ACD:S△BCA=4:9,若AC=6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com