科目： 来源： 题型：

如图，⊙O的圆心在Rt△ABC的直角边AC上，⊙O经过C、D两点，与斜边AB交于点E，连接BO、ED，有BO∥ED，作弦EF⊥AC于G，连接DF．
（1）求证：AB为⊙O的切线；
（2）若⊙O的半径为5，sin∠DFE=

3

5

，求EF的长．

科目： 来源： 题型：

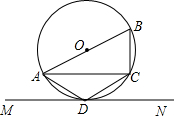如图所示，AB是⊙O的直径，D是圆上一点，

AD

=

DC

，连接AC，过点D作弦AC的平行线MN．
（1）证明：MN是⊙O的切线；
（2）已知AB=10，AD=6，求弦BC的长．

科目： 来源： 题型：

如图，AB是半圆的直径，O为圆心，AD、BD是半圆的弦，且∠PDA=∠PBD．
（1）判断直线PD是否为⊙O的切线，并说明理由；
（2）如果∠BDE=60°，PD=

3

，求PA的长．

科目： 来源： 题型：

已知“6”字形图中，FM是大⊙O的直径，BC与大⊙O相切于B，OB与小⊙O相交于A，AD∥BC，CD∥BH∥FM，DH⊥BH于H，设∠FOB=30°，OB=4，BC=6．
﹙1﹚求证：AD为小⊙O的切线；
﹙2﹚求DH的长．﹙结果保留根号﹚

科目： 来源： 题型：

如图，A、B是⊙O上的两点，∠AOB=120°，点D为劣弧

AB

的中点．
（1）求证：四边形AOBD是菱形；
（2）延长线段BO至点P，交⊙O于另一点C，且BP=3OB，求证：AP是⊙O的切线．

科目： 来源： 题型：

如图，一块四边形土地，其中∠ABD=120°，AB⊥AC，BD⊥CD，AB=30

3

m，CD=50

3

m，求这块土地的面积．

科目： 来源： 题型：

27、某学校的大门是伸缩的推拉门，如图是大门关闭时的示意图．若图中菱形的边长都是0.5米、锐角都是50°，则大门的宽大约是多少米？（结果保留两个有效数字）
（参考数据：sin25°=0.4226，cos25°=0.9063）

科目： 来源： 题型：阅读理解

图①，②是晓东同学在进行“居民楼高度、楼间距对住户采光影响问题”的研究时画的两个示意图．请你阅读相关文字，解答下面的问题．
（1）图①是太阳光线与地面所成角度的示意图．冬至日正午时刻，太阳光线直射在南回归线（南纬23.5°）B地上．在地处北纬36.5°的A地，太阳光线与地面水平线l所成的角为α，试借助图①，求α的度数；
（2）图②是乙楼高度、楼间距对甲楼采光影响的示意图．甲楼地处A地，其二层住户的南面窗户下沿距地面3.4米．现要在甲楼正南面建一幢高度为22.3米的乙楼，为不影响甲楼二层住户（一层为车库）的采光，两楼之间的距离至少应为多少米？

科目： 来源： 题型：

如图，某居民小区内有一块梯形形状的空地ABCD，今量得∠A=∠D=120°，AB=AD=20米，居民们筹集了5400元钱准备在空地上种植玫瑰花．已知种植一平方米玫瑰花需要10元钱，居民们筹集的资金够用吗？（参考数据：

2

≈1.414，

3

≈1.732）

科目： 来源： 题型：

18、小刚有一块含有30°角的直角三角板，他想测量其短直角边的长度，而手中另外只有一个量角器，于是他采用了如下的方法，并获得了相关数据：
第一步，他先用三角板标有刻度的一边测出量角器的直径AB的长度为9cm；
第二步，将三角板与量角器按如图所示的方式摆放，并量得∠BOC为80°（O为AB的中点）．
请你根据小刚测得的数据，求出三角板的短直角边AC的长．
（参考数据：sin80°=0.98，cos80°=0.17，tan80°=5.67；sin40°=0.64，cos40°=0.77，tan40°=0.84，结果精确到0.1cm）