科目： 来源： 题型：

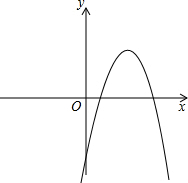已知一元二次方程-x²+bx+c=0的两个实数根是m，4，其中0＜m＜4．
（1）求b、c的值（用含m的代数式表示）；
（2）设抛物线y=-x²+bx+c与x轴交于A、B两点，与y轴交于点C．若点D的坐标为（0，-2），且AD•BD=10，求抛物线的解析式及点C的坐标；
（3）在（2）中所得的抛物线上是否存在一点P，使得PC=PD？若存在，求出P点的坐标；若不存在，请说明理由．

科目： 来源： 题型：

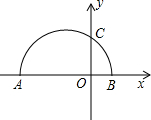如图，已知两点A（-8，0），C（0，4），以AB为直径的半圆与y轴正半轴交于点C．
（1）求过A、C两点的直线的解析式和经过A、B、C三点的抛物线的解析式；
（2）若点D是（1）中抛物线的顶点，求△ACD的面积．

科目： 来源： 题型：

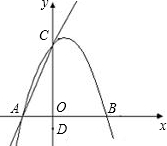如图，已知抛物线y=ax²+bx+c与x轴交于A（k，0）（k＜0）、B（3，0）两点，与y轴正半轴交于C点，且tan∠CAO=3．
（1）求此抛物线的解析式（系数中可含字母k）；
（2）设点D（0，t）在x轴下方，点E在抛物线上，若四边形ADEC为平行四边形，试求t与k的函数关系式；
（3）若题（2）中的平行四边形ADEC为矩形，试求出D的坐标．

科目： 来源： 题型：

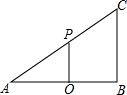如图，在△ABC中，∠B=90°，AB=4，BC=3，O是AB的中点，OP⊥AB交AC于点P．
（1）证明线段AO、OB、OP中，任意两条线段长度之和大于第三条线段的长度；
（2）过线段OB（包括端点）上任一点M，作MN⊥AB交AC于点N．如果要使线段AM、MB、MN中任意两条线段长度之和大于第三条线段的长度，那么请求出线段AM的长度的取值范围．

科目： 来源： 题型：

如图，梯子AB斜靠在墙上，∠ACB=90°，AB=5米，BC=4米，当点B下滑到点B′时，点A向左平移到点A′．设BB′=x米（0＜x＜4），AA′=y米．
（1）用含x的代数式表示y；
（2）当x为何值时，点B下滑的距离与点A向左平移的距离相等？
（3）请你对x再取几个值，计算出对应的y值，并比较对应的y值与x值的大小（y值可以用精确到0.01的近似数表示，也可用无理数表示）．
（4）根据第（1）～（3）题的计算，还可以结合画图、观察，推测y与x的大小关系及对应的x的取值范围．

科目： 来源： 题型：

已知：如图，以△ABC的BC边为直径的半圆交AB于D，交AC于E，过E点作EF⊥BC，垂足为F，且BF：FC=5：1，AB=8，AE=2．求EC的长．

科目： 来源： 题型：

14、如图，是十堰市郧县汉江斜拉桥的剖面图．BC是桥面，AD是桥墩，设计大桥时工程师要求斜拉的钢绳AB等于AC．大桥建成后，工程技术人员要对大桥质量进行验收，由于桥墩AD很高，无法直接测量钢绳AB、AC的长度．请你用三种方法检验AB、AC的长度是否相等．（检验工具为刻度尺、量角器；检验时，人只能站在桥面上）

科目： 来源： 题型：

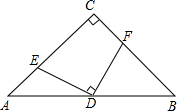已知：如图，在Rt△ABC中，∠ACB=90°，AC=BC，D是AB的中点，E、F分别在AC、BC上，且ED⊥FD．求证：S_{四边形EDFC}=

1

2

S_△ABC．

科目： 来源： 题型：

5、已知：如图，在四边形ABCD中，E是AC上一点，∠1=∠2，∠3=∠4．求证：∠5=∠6．

科目： 来源： 题型：

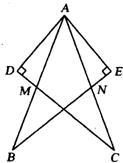2、如图，在△ABE和△ACD中，给出以下四个论断：
（1）AB=AC；（2）AD=AE；（3）AM=AN；（4）AD⊥DC，AE⊥BE．
以其中三个论断为题设，填入下面的“已知”栏中，一个论断为结论，填入下面的“求证”栏中，使之组成一个真命题，并写出证明过程．