
已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿BD将△BCD翻折到△![]() ,使得平面
,使得平面![]() ⊥平面ABD.
⊥平面ABD.
(Ⅰ)求证:![]() 平面ABD;
平面ABD;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)求二面角![]() 的余弦值.
的余弦值.
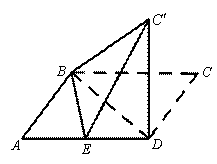
证明:(Ⅰ)平行四边形ABCD中,AB=6,AD=10,BD=8,
沿直线BD将△BCD翻折成△![]()
可知CD=6,BC’=BC=10,BD=8,
即![]() ,
,
故![]() . ………………2分
. ………………2分
∵平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]()
![]() 平面
平面![]() =
=![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() . ………………5分
. ………………5分
(Ⅱ)由(Ⅰ)知![]() 平面ABD,且
平面ABD,且![]() ,
,
如图,以D为原点,建立空间直角坐标系![]() . ………………6分
. ………………6分
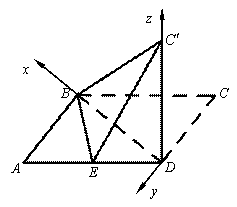 则
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
∵E是线段AD的中点,
∴![]() ,
,![]() .
.
在平面![]() 中,
中,![]() ,
,![]() ,
,
设平面![]() 法向量为
法向量为![]() ,
,
∴ 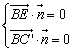 ,即
,即![]() ,
,
令![]() ,得
,得![]() ,故
,故![]() . ………………8分
. ………………8分
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则
![]() . ………………9分
. ………………9分
∴ 直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() . ………………10分
. ………………10分
(Ⅲ)由(Ⅱ)知平面![]() 的法向量为
的法向量为![]() ,
,
而平面![]() 的法向量为
的法向量为![]() ,
,
∴ ![]() ,
,
因为二面角![]() 为锐角,
为锐角,
所以二面角![]() 的余弦值为
的余弦值为![]() . ………………13分
. ………………13分


科目:高中数学 来源: 题型:
| OA |
| a |
| OB |
| b |
| OC |
| c |
| OH |
| h |
| a |
| b |
| c |
| h |
| AH |
| BC |
| h |
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)如图,求证:DE是⊙O的切线;
(2)连结OE、AE,当∠CAB为何值时,四边形AOED是平行四边形,并在此条件下求sin∠CAE的值.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| OA |
| a |
| OB |
| b |
| OC |
| c |
| OH |
| h |
| a |
| b |
| c |
| h |
| AH |
| BC |
| h |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年辽宁省沈阳二中高一(下)期中数学试卷(必修4)(解析版) 题型:解答题
 ,试用
,试用 表示
表示 ;
; ;
; .
.查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省肇庆市南丰中学高三(上)数学复习试卷C (必修4)(解析版) 题型:解答题
 ,试用
,试用 表示
表示 ;
; ;
; .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com