练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图2-6-22,已知PM是⊙O的切线,M为切点,PAB和PCD均是⊙O割线,且AB·PD=BC·AD.

    求证:PM2-PA2=AC·AD.

    图2-6-22

    证明:∵=,

    ∴∠ADC=∠ABC.

    ∵AB·PD=BC·AD,∴.

    ∴△ABC∽△ADP.∴∠ACB=∠APD.

    又∵=,∴∠ACB=∠ADB.

    ∴∠APC=∠ADB.

    又∵四边形ABDC内接于圆,

    ∴∠ACP=∠ABD.

    ∴△APC∽△ADB.

    ∴.

    ∴AP·AB=AC·AD.

    由切割线定理,得PM2=PA·PB.

    ∴PM2-PA2=PA·PB-PA2

    =PA(PB-PA)=PA·AB=AC·AD.

    ∴PM2-PA2=AC·AD.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
    A．（不等式选做题）不等式|x-5|+|x+3|≥10的解集是
    （-∞，-4]∪[6，+∞）
    （-∞，-4]∪[6，+∞）
    ．
    B．（坐标系与参数方程选做题）在极坐标系中，圆ρ=-2sinθ的圆心的极坐标是
    （1，
    3π
    2
    ）
    （1，
    3π
    2
    ）
    ．
    C．（几何证明选做题）如图，已知圆中两条弦AB与CD相交于点F，E是AB延长线上一点，且DF=CF=2
    		2
    ，BE=1，BF=2，若CE与圆相切，则线段CE的长为
    		7
    		7
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，某城市设立以城中心O为圆心、r公里为半径的圆形保护区，从保护区边缘起，在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC，现要在保护区边缘PQ弧上选择一点A作为出口，建一条连接两条公路且与圆O相切的直道BC．已知通往一级公路的道路AC每公里造价为a万元，通往高速公路的道路AB每公里造价是m2a万元，其中a，r，m为常数，设∠POA=θ，总造价为y万元．
    （1）把y表示成θ的函数y=f（θ），并求出定义域；
    （2）当m=
    		6
    +
    		2
    2
    时，如何确定A点的位置才能使得总造价最低？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

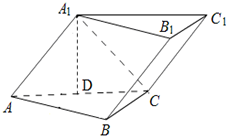    如图，已知斜三棱柱（侧棱不垂直于底面）ABC-A1B1C1的侧面A1ACC1与底面ABC垂直，BC=2，AC=2
    		3
    ，AB=2
    		2
    ，AA1=A1C=
    		6
    ．
    （Ⅰ） 设AC的中点为D，证明A1D⊥底面ABC；
    （Ⅱ） 求异面直线A1C与AB成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某篮球运动员参加了10场比赛，他每专场比赛得分的茎叶图如图所示，已知他得分的中位数为22分，若要使他得分的方差最小，则a=
    2
    2
    ，b=
    2
    2
    ．
    茎 叶 　
    1 2  3  3  7
    2 a  b  5  6  8
    3 0  

    查看答案和解析>>

    同步练习册答案