
(1)求b与c的关系式(用c表示b);
(2)设函数F(x)=f(x)g(x)在(-¥,+¥)内有极值点,求c的取值范围.
| 本小题考查导数、切线、极值等知识及综合运用数学知识解决问题的能力
解:(1)依题意,令f(x)=g¢(x),得2x+b=1,故x= 由于 ∵ b>-1,c>0,∴ b=-1+ (2)F(x)=f(x)g(x)=x3+2bx2+(b2+c)x+bc. ∴ F¢(x)=3x2+4bx+b2+c.令F¢(x)=0,即3x2+4bx+b2+c=0. 则D=16b2-12(b2+c)=4(b2-3c) 若D=0,则F¢(x)=0有一个实数根x0,且F¢(x)的变化如下:
于是x=x0不是函数F(x)的极值点. 若D>0,则F¢(x)=0有两个不相等的实根x1、x2(x1<x2),且F¢(x)的变化如下:
由此x=x1是函数F(x)的极大值点,是x=x2函数F(x)的极小值点. 综上所述,当且仅当D>0时,函数F(x)在(-¥,+¥)上有极值点. 由D=4(b2-3c)>0得b< ∵ b=-1+ 解之得0<c<7- 故所求c的取值范围是(0,7- |


科目:高中数学 来源: 题型:044
已知b>-1,c>0,函数f(x)=x+b的图像与函数g(x)=x2+bx+c的图像相切.
(1)求b与c的关系式(用c表示b);
(2)设函数F(x)=f(x)g(x)在(-¥,+¥)内有极值点,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知b>-1,c>0,函数![]() 的图象与函数
的图象与函数![]() 的图象相切.
的图象相切.
(Ⅰ)设![]()
(Ⅱ)是否存在常数c,使得函数![]() 内有极值点?若存在,求出c的取值范围;若不存在,请说明理由.
内有极值点?若存在,求出c的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届广东省高一下学期期末考试数学试卷(解析版) 题型:填空题
已知b>0,直线b2x+y+1=0与ax-(b2+4)y+2=0互相垂直,则ab的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三5月高考冲刺理科数学试卷(解析版) 题型:解答题
已知m>1,直线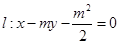 ,椭圆C:
,椭圆C: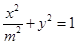 ,
,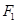 、
、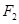 分别为椭圆C的左、右焦点.
分别为椭圆C的左、右焦点.
(Ⅰ)当直线过右焦点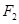 时,求直线的方程;
时,求直线的方程;
(Ⅱ)设直线与椭圆C交于A、B两点,△A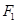
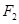 、△B
、△B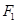
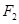 的重心分别为G、H.若原点O在以线段GH为直径的圆内,求实数m的取值范围.
的重心分别为G、H.若原点O在以线段GH为直径的圆内,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com