解:(I)可得抛物线的准线方程为
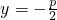
,由题意可得

,解得
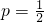
.
∴抛物线的方程为x
2=y.把点A(a,4)代人此方程得a
2=4,解得a=±2.
∴a=±2,
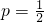
.
(II)由题意可知:过点P(t,t
2)的直线PQ的斜率k不为0,则直线PQ:y-t
2=k(x-t),
当y=0时,

,∴M

.
联立

消去y得(x-t)[x-(k-t)]=0,
解得x=t,或x=k-t.∴Q(k-t,(k-t)
2),
∵QN⊥QP,∴

,∴直线NQ:

,
联立

,消去y化为

,解得x=k-t,或

.
∴N

,∴抛物线在点N处的切线的斜率为

=

,
另一方面k
MN=

,
∴

,
∵

,∴

,化为k
2+tk-2t
2=-1为定值.
分析:(I)利用抛物线的定义和点在抛物线上满足的条件即可得出;
(II)由题意可知:过点P(t,t
2)的直线PQ的斜率k不为0,则直线PQ:y-t
2=k(x-t),即可求出点M的坐标,把直线PQ的方程与抛物线的方程联立即可得出点Q的坐标.由QN⊥QP,即可得出直线QN的方程,与抛物线方程联立即可得出点N的坐标,利用导数和斜率的计算公式即可得出直线MN两种形式的斜率,化简即可证明结论.
点评:熟练掌握抛物线的定义及其性质、直线与抛物线相交问题转化为方程联立即可得到交点的坐标、导数的几何意义与切线的斜率关系、斜率的计算公式设解题的关键.

 已知抛物线C:x2=2py(p>0)上一点A(a,4)到其准线的距离为
已知抛物线C:x2=2py(p>0)上一点A(a,4)到其准线的距离为 .
.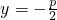 ,由题意可得
,由题意可得 ,解得
,解得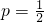 .
.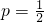 .
. ,∴M
,∴M .
. 消去y得(x-t)[x-(k-t)]=0,
消去y得(x-t)[x-(k-t)]=0, ,∴直线NQ:
,∴直线NQ: ,
, ,消去y化为
,消去y化为 ,解得x=k-t,或
,解得x=k-t,或 .
. ,∴抛物线在点N处的切线的斜率为
,∴抛物线在点N处的切线的斜率为 =
= ,
, ,
, ,
, ,∴
,∴ ,化为k2+tk-2t2=-1为定值.
,化为k2+tk-2t2=-1为定值.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案