练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    函数f(x)=
    		9-x
    +
    (x-1)0
    		x+4
    定义域为
     
    ．
    分析：根据函数有意义的条件可得
    9-x≥0
    x-1≠0
    x+4＞0
    解不等式組可求函数的定义域．
    解答：解：根据函数有意义的条件可得
    9-x≥0
    x-1≠0
    x+4＞0

    解不等式組可得，
    x≤9
    x≠1
    x＞-4

    故答案为：{x|-4＜x＜9且x≠1}
    点评：本题主要考查了含有偶次根式及分式、x0的形式的函数定义域的求解，属于基础试题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    探究函数f(x)=2x+
    8
    x
    ，x∈(0，+∞)    的最小值，并确定取得最小值时x的值．列表如下：
    x … 0.5 1 1.5 1.7 1.9 2 2.1 2.2 2.3 3 4 5 7 …
    y … 16 10 8.34 8.1 8.01 8 8.01 8.04 8.08 8.6 10 11.6 15.14 …
    请观察表中y值随x值变化的特点，完成以下的问题．
    （1）函数f(x)=2x+
    8
    x
    (x＞0)    在区间（0，2）上递减；函数f(x)=2x+
    8
    x
    (x＞0)    在区间
    （2，+∞）
    （2，+∞）
    上递增．当x=
    2
    2
    时，y最小=
    4
    4
    ．
    （2）证明：函数f(x)=2x+
    8
    x
    (x＞0)    在区间（0，2）递减．
    （3）思考：函数f(x)=2x+
    8
    x
    (x＜0)    时，有最值吗？是最大值还是最小值？此时x为何值？（直接回答结果，不需证明）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    探究函数f（x）=x+
    4
    x
    ，x∈（0，+∞）的最小值，并确定取得最小值时x的值．列表如下：
    x … 0.5 1 1.5 1.7 1.9 2 2.1 2.2 2.3 3 4 5 7 …
    y … 8.5 5 4.17 4.05 4.005 4 4.005 4.02 4.04 4.3 5 5.8 7.57 …
    请观察表中值y随x值变化的特点，完成以下的问题．
    函数f（x）=x+
    4
    x
    （x＞0）在区间（0，2）上递减；
    函数f（x）=x+
    4
    x
    （x＞0）在区间
    （2，0）
    （2，0）
    上递增．
    当x=
    2
    2
    时，y最小=
    4
    4
    ．
    证明：函数f（x）=x+
    4
    x
    （x＞0）在区间（0，2）递减．
    思考：（直接回答结果，不需证明）
    （1）函数f（x）=x+
    4
    x
    （x＜0）有没有最值？如果有，请说明是最大值还是最小值，以及取相应最值时x的值．
    （2）函数f（x）=ax+
    b
    x
    ，（a＜0，b＜0）在区间
    [-
    b
    a
    ，0）
    [-
    b
    a
    ，0）
     和
    （0，
    b
    a
    ]
    （0，
    b
    a
    ]
    上单调递增．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    探究函数f（x）=x+
    4
    x
    ，x∈（-∞，0）的最大值，并确定取得最大值时x的值．列表如下：
    x … -3 -2.3 -2.2 -2.1 -2 -1.9 -1.7 -1.5 -1 -0.5 …
    y … -4.3 -4.04 -4.02 -4.005 -4 -4.005 -4.05 -4.17 -5 -8.5 …
    请观察表中y值随x值变化的特点，完成以下的问题．
    （1）函数f（x）=x+
    4
    x
    ，x∈（-∞，0）在区间
     
    上为单调递增函数．当x=
     
    时，f（x）最大=
     
    ．
    （2）证明：函数f（x）=x+
    4
    x
    在区间[-2，0）为单调递减函数．

    查看答案和解析>>

    科目：高中数学 来源：2013年湖北新洲、红安、麻城一中高三上学期期末考文科数学试卷（解析版） 题型：选择题

    对于函数f (x)和g(x)，其定义域为[a, b]，若对任意的x∈[a, b]总有|1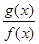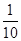－|≤，则称f (x)可被g(x)置换，那么下列给出的函数中能置换f (x)= 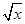x∈[4，16]的是 (    )

    A．g(x)=2x+6 x∈[4，16]                    B．g(x)=x2+9 x∈[4，16]

    C．g(x)= 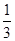(x+8) x∈[4，16]                 D．g(x)=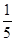(x+6) x∈[4，16]

     

    查看答案和解析>>

    同步练习册答案