练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    双曲线-y2=1上有动点P，F1、F2是两个焦点，求△PF1F2的重心M的轨迹方程.

    思路解析：判断轨迹形状，得解法一；点M是被动点，P是主动点且在已知曲线上得解法二相关点法（中间变量法）.

    解法一：（待定系数法）如图所示.

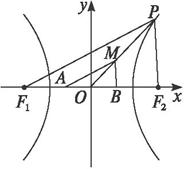
    ∵M是△PF1F2的重心，∴|OM|=|OP|.

    过M作MA∥PF1交x轴于A,过M作MB∥PF2交x轴于B.∴|PF1|=3|MA|，|PF2|=3|MB|.

    ∵P在双曲线上，

    ∴||PF1|-|PF2||=2a=6.

    ∴|3|MA|-3|MB||=6.

    ∴||MA|-|MB||=2＜=|AB|.

    ∴点M是以A、B为焦点的双曲线，设其标准方程是-=1(a＞0，b＞0).

    则2a=2,2c=|AB|=.

    ∴a2=1,b2=c2-a2=（）2-1=.

    ∴点M的轨迹方程是x2-=1(y≠0).

    解法二：（相关点法）设M（x,y）,P(x0,y0).

    ∵M是△PF1F2的重心，

    ∴M分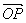Equation.3的比λ=.

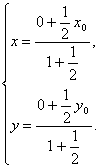    ∴解得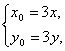即P（3x,3y）.

    ∵P在双曲线上，

    ∴-(3y)2=1.

    ∴点M在轨迹方程是x2-=1（y≠0）.

    深化升华

        当动点M随点P变化而变化时，点P在已知曲线上，求动点M的轨迹方程，常利用相关点法（中间变量代入法）.当题目中出现重心时，常用重心的性质：到顶点距离是到对边中点距离的二倍；三角形重心坐标公式.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    给出以下命题：
    （1）α，β表示平面，a，b，c表示直线，点M；若a?α，b?β，α∩β=c，a∩b=M，则M∈c；
    （2）平面内有两个定点F1（0，3），F2（0-3）和一动点M，若||MF1|-|MF2||=2a（a＞0）是定值，则点M的轨迹是双曲线；
    （3）在复数范围内分解因式：x2-3x+5=(x-
    3+
    		11
    i
    2
    )(x-
    3-
    		11
    i
    2
    )    ；
    （4）抛物线y2=12x上有一点P到其焦点的距离为6，则其坐标为P（3，±6）．
    以上命题中所有正确的命题序号为
    （1）（3）（4）
    （1）（3）（4）
    ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    给出以下命题：
    （1）α，β表示平面，a，b，c表示直线，点M；若a?α，b?β，α∩β=c，a∩b=M，则M∈c；
    （2）平面内有两个定点F1（0，3），F2（0-3）和一动点M，若||MF1|-|MF2||=2a（a＞0）是定值，则点M的轨迹是双曲线；
    （3）在复数范围内分解因式：x2-3x+5=(x-
    3+
    		11
    i
    2
    )(x-
    3-
    		11
    i
    2
    )    ；
    （4）抛物线y2=12x上有一点P到其焦点的距离为6，则其坐标为P（3，±6）．
    以上命题中所有正确的命题序号为______．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年湖南师大附中高二（上）期中数学试卷（理科）（解析版） 题型：解答题

    已知椭圆C：与双曲线-y2=1有公共焦点，且离心率为．A，B分别是椭圆C的左顶点和右顶点．点S是椭圆C上位于x轴上方的动点．直线AS，BS分别与直线l：x=分别交于M，N两点．
    （1）求椭圆C的方程；
    （2）延长MB交椭圆C于点P，若PS⊥AM，试证明MS2=MB•MP．
    （3）当线段MN的长度最小时，在椭圆C上是否存在点T，使得△TSB的面积为？若存在确定点T的个数，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2005年浙江省杭州市高考数学二模试卷（文科）（解析版） 题型：解答题

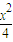    设双曲线-y2=1的右顶点为A，P是双曲线上异于顶点的一个动点，从A引双曲线的两条渐近线的平行线与直线OP （O为坐标原点）分别交于Q和R两点．
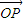    （1）证明：无论P点在什么位置，总有||2=|•|；
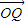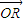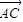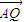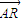    （2）设动点C满足条件：=（+），求点C的轨迹方程．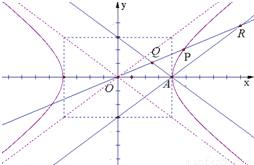

    查看答案和解析>>

    同步练习册答案