
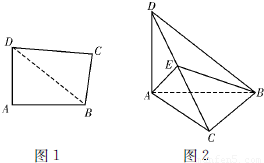
 如图l,四边形ABCD中,AB=AD,AB⊥AD,DC⊥BC,将△DCB沿BD折起,使AC⊥BC,如图2.点E在DC上,AE=
如图l,四边形ABCD中,AB=AD,AB⊥AD,DC⊥BC,将△DCB沿BD折起,使AC⊥BC,如图2.点E在DC上,AE=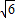 且AE⊥DC,若二面角A-BD-C的正弦值为
且AE⊥DC,若二面角A-BD-C的正弦值为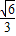 .
.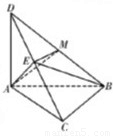 证明:(1)∵AC⊥BC,DC⊥BC,AC∩DC=C
证明:(1)∵AC⊥BC,DC⊥BC,AC∩DC=C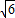 ,AM=
,AM=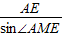 =
=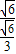 =3,EM=
=3,EM=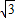
 •
• •EM•DB•AE=3
•EM•DB•AE=3


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
 请考生在第(1),(2),(3)题中任选一题作答,如果多做,则按所做的第一题记分.
请考生在第(1),(2),(3)题中任选一题作答,如果多做,则按所做的第一题记分.| BF |
| FC |
| π |
| 6 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
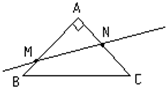 如图,△ABC是斜边为2的等腰直角三角形,点M,N分别为AB、AC上的点,过M、N的直线l将该三角形分成周长相等的两部分.
如图,△ABC是斜边为2的等腰直角三角形,点M,N分别为AB、AC上的点,过M、N的直线l将该三角形分成周长相等的两部分.查看答案和解析>>
科目:高中数学 来源: 题型:022

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
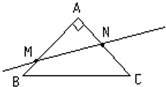 如图,△ABC是斜边为2的等腰直角三角形,点M,N分别为AB、AC上的点,过M、N的直线l将该三角形分成周长相等的两部分.
如图,△ABC是斜边为2的等腰直角三角形,点M,N分别为AB、AC上的点,过M、N的直线l将该三角形分成周长相等的两部分.查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°, ∠B =60°,BC=2.点0是AC的中点,过点0的直线l从与AC重合的位置开始,绕点0作逆时针旋转,交AB边于点D.过点C作CE∥AB交直线l于点E,设直线l的旋转角为α.
(1) ①当α=________度时,四边形EDBC是等腰梯形,此时AD的长为_________;②当α=________度时,四边形EDBC是直角梯形,此时AD的长为_________;
(2)当α=90°时,判断四边形EDBC是否为菱形,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com