

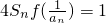 ,求证:-
,求证:- <
< <-
<- ;
; ,Tn为数列 {bn} 的前n项和,求证:T2012-1<ln2012<T2011.
,Tn为数列 {bn} 的前n项和,求证:T2012-1<ln2012<T2011. 的定义域为{x|x≠1}
的定义域为{x|x≠1}
 ,当n≥2时,2
,当n≥2时,2
 .
.
 =t.则t>1,x=
=t.则t>1,x=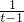

 ,x>0 ①
,x>0 ① ,h′(t)=
,h′(t)= 由t∈(1,+∞)知h′(t)>0
由t∈(1,+∞)知h′(t)>0
 ,x>0 ②
,x>0 ② ,x>0
,x>0  ,即
,即 
 则
则 
 中令n=1,2,3…..2010,2011并将各式相加得
中令n=1,2,3…..2010,2011并将各式相加得
 的定义域,再求其导数,由f′(x)<0解出单调减区间即可;
的定义域,再求其导数,由f′(x)<0解出单调减区间即可; ,再由此式得到2
,再由此式得到2 ,两式相减得结合已知条件得出an的通项公式,于是,待证不等式即为
,两式相减得结合已知条件得出an的通项公式,于是,待证不等式即为 .为此,我们考虑证明不等式
.为此,我们考虑证明不等式 ,下面利用换元法结合导数工具进行证明.
,下面利用换元法结合导数工具进行证明. 则
则  ,下面只须在
,下面只须在 中令n=1,2,3…..2010,2011并将各式相加即可.
中令n=1,2,3…..2010,2011并将各式相加即可.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•卢湾区一模)已知函数f(x)=
(2012•卢湾区一模)已知函数f(x)=| x+1-t | t-x |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•卢湾区一模)已知函数f(x)=
(2012•卢湾区一模)已知函数f(x)=| x+1-t | t-x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 )<
)< ,则称f(x)为定义在D上的C函数.
,则称f(x)为定义在D上的C函数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com