
| 1 |
| 2 |
| S1 |
| S |
| 1400 |
| 1600 |
| 7 |
| 8 |
| 7 |
| 8 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013届四川省成都外国语学校高二下学期期中考试数学试卷(解析版) 题型:选择题
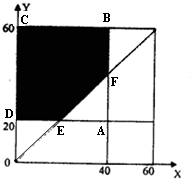
在一次商贸交易会上,商家在柜台开展促销抽奖活动,甲、乙两人相约同一天上午去该柜台参与抽奖. 若甲计划在9:00~9:40之间赶到,乙计划在9:20~10:00之间赶到,则甲比乙提前到达的概率为( )

A. B.
B. C.
C. D.
D. 
查看答案和解析>>
科目:高中数学 来源:2011年高考数学必做100题(必修3)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:
在一次商贸会上,甲、乙两人相约同一天上午前去洽谈,若甲计划在9:00-9:40之间赶到,乙计划在9:20-10:00之间赶到,求甲比乙提前到达的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com