练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知图是函数的图象上的一段，则

    [　　]

    A．＝，＝

    B．＝，＝－

    C．＝2，＝

    D．＝2，＝－

    答案：C
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数是定义在上的奇函数，当时，（为常数）。

    （1）求函数的解析式；

    （2）当时，求在上的最小值，及取得最小值时的，并猜想在上的单调递增区间（不必证明）；

    （3）当时，证明：函数的图象上至少有一个点落在直线上。

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山东临沂高三5月高考模拟文科数学试卷（解析版） 题型：解答题

    已知点是函数的图象上一点，数列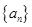的前n项和.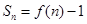

    （Ⅰ）求数列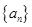的通项公式；

    （Ⅱ）将数列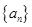前2013项中的第3项，第6项， ，第3k项删去，求数列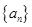前2013项中剩余项的和.

     

    查看答案和解析>>

    科目：高中数学 来源：2013届浙江省台州市高二下学期期末考试文科数学试卷（解析版） 题型：填空题

    已知点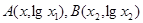是函数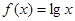的图象上任意不同两点，依据图象可知，段段AB总是位于A,B两点之间函数图象的下方，因此有结论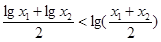成立。运用类比思想方法可知，若点，是函数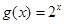的图象上的不同两点，则类似地有成立    。

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知图是函数的图象上的一段，则（　　 ）

    Ａ．      Ｂ．              

    Ｃ．     Ｄ．

    查看答案和解析>>

    同步练习册答案