解:(Ⅰ)

,令N(x)=(1+x)
2-1+ln(1+x)∴N′(x)>0,故N(x)在(-1,+∞)上单调递增,N(0)=0,又函数f(x)在(-1,0)上单调减,(0,+∞)上单调递增,故f(x)
min=f(0)=0
(Ⅱ)由题意f(x)在[0,+∞)上单调递增,故
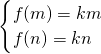
,即方程f(x)=kx在[0,+∞)上有两个不相等的实数根,又0是方程f(x)=kx的根,故此方程还有一个正根.
令

,∴

,
令N
1(x)=(1-k)(1+x)
2-1+ln(1+x),
当0<k<1时,N
1′(x)>0,故N
1(x)单调递增,由于当x→+∞时,F(x)→+∞,F(0)=0,要使F(x)=0有一个正根,只要F(x)有一个正德极值,即N
1(x)=0有一个正根,故N
1(x)<0,即-k<0,∴0<k<1;
当k≥1时,令F(0)=0则

,由于x>0,∴(1-k)x≤0,而

故上式不成立
综上所述,0<k<1
分析:(Ⅰ) 先求导函数,再令N(x)=(1+x)
2-1+ln(1+x)∴N′(x)>0,故N(x)在(-1,+∞)上单调递增,结合f(x)在(-1,0)上单调减,(0,+∞)上单调递增可求f(x)的最小值.
(Ⅱ)对于存在性问题,可先假设存在,即假设存在区间[m,n](m<n),再利用二次函数的单调性,求出m,n的值,若出现矛盾,则说明假设不成立,即不存在;否则存在.
点评:本小题主要考查利用导数研究函数的单调性、考查利用导数求闭区间上函数的最值等基础知识,考查等价转化问题的能力,有一定的难度.属于中档题.


 ,令N(x)=(1+x)2-1+ln(1+x)∴N′(x)>0,故N(x)在(-1,+∞)上单调递增,N(0)=0,又函数f(x)在(-1,0)上单调减,(0,+∞)上单调递增,故f(x)min=f(0)=0
,令N(x)=(1+x)2-1+ln(1+x)∴N′(x)>0,故N(x)在(-1,+∞)上单调递增,N(0)=0,又函数f(x)在(-1,0)上单调减,(0,+∞)上单调递增,故f(x)min=f(0)=0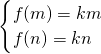 ,即方程f(x)=kx在[0,+∞)上有两个不相等的实数根,又0是方程f(x)=kx的根,故此方程还有一个正根.
,即方程f(x)=kx在[0,+∞)上有两个不相等的实数根,又0是方程f(x)=kx的根,故此方程还有一个正根. ,∴
,∴ ,
, ,由于x>0,∴(1-k)x≤0,而
,由于x>0,∴(1-k)x≤0,而 故上式不成立
故上式不成立

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<