

| 22•sin49°48′ |
| 26 |
| BC |
| sin∠CAB |
| AC |
| sin∠ABC |
| 22x |
| sin(49°48′-α) |
| 26x |
| sin(180°-49°48′) |
| 22•sin49°48′ |
| 26 |
. |
| 1 |


科目:高中数学 来源: 题型:
 如图,某海域中有甲、乙两艘测量船分别停留在相距(
如图,某海域中有甲、乙两艘测量船分别停留在相距(| 6 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
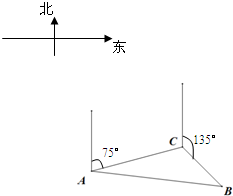 如图,甲船在A处测得:“乙船位于北偏东75°,距离为10海里的C处,并正沿着北偏东135°的方向,以每小时12海里的速度驶去.”经过半小时,甲船在B处追上了乙船.求:
如图,甲船在A处测得:“乙船位于北偏东75°,距离为10海里的C处,并正沿着北偏东135°的方向,以每小时12海里的速度驶去.”经过半小时,甲船在B处追上了乙船.求:查看答案和解析>>
科目:高中数学 来源:教材完全解读 高中数学 必修5(人教B版课标版) 人教B版课标版 题型:044
甲船在A处遇险,在甲船正西南10海里B处的乙船收到甲船的报警后,测得甲船是沿着方位角105°的方向,以每小时9海里的速度向某岛靠近,如果乙船要在40分钟内追上甲船,则乙船应以多大速度,以何方位角航行?
[注]方位角:从某点开始的指北方向按顺时针转到目标方向线为止的水平角叫方位角
查看答案和解析>>
科目:高中数学 来源:1965年全国统一高考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com