
![]()
【解】(1)由![]() =λ
=λ![]() +(1-λ)
+(1-λ)![]() 得到
得到![]() =λ
=λ![]() ,
,
所以B,N,A三点共线, ……………………2分
又由x=λ x1+(1-λ) x2与向量![]() =λ
=λ![]() +(1-λ)
+(1-λ)![]() ,得N与M的横坐标相同. ……………4分
,得N与M的横坐标相同. ……………4分
对于 [0,1]上的函数y=x2,A(0,0),B(1,1),
则有![]() ,故
,故![]() ;
;
所以k的取值范围是![]() . ………
. ………![]() ……………6分
……………6分
(2)对于![]() 上的函数
上的函数![]() ,
,
A(![]() ),B(
),B(![]() ), ……………………8分则直线AB的方程
), ……………………8分则直线AB的方程![]() , ……………………10分
, ……………………10分
令![]() ,其中
,其中![]() ,
,
于是![]() , ……………………13分
, ……………………13分
列表如下:
| x | em | (em,em+1-em) | em+1-em | (em+1-em,em+1) | em+1 |
|
| + | 0 | - | ||
|
| 0 | 增 |
| 减 | 0[来源:学_科_网] |
则![]()
![]() ,且在
,且在![]() 处取得最大值,
处取得最大值,
又![]() 0.123
0.123![]() ,从而命题成立. ……………………16分
,从而命题成立. ……………………16分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
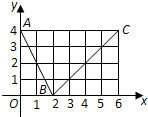 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=| lim |
| △x→0 |
| f(1+△x)-f(1) |
| △x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com