

(1)求证:MN∥平面PAD;(2)求证:MN⊥CD.
(3)若∠PDA=45°,求证:MN⊥平面PCD.
|
【探究】 (1)要证明MN∥平面PAD,须证MN平行于平面PAD内某一条直线.注意到M,N分别为AB,PC的中点,可取PD的中点E,从而只须证明MN∥AE即可,证明如下:
证明:取PD的中点E, 连结AE、EN. 则EN 故AMNE为平行四边形,∴MN∥AE. ∵AE (2)要证MN⊥CD,可证MN⊥AB. 由问(1)知,需证AE⊥AB. ∵PA⊥平面ABCD.∴PA⊥AB,又AD⊥AB, ∴AB⊥平面PAD,∴AB⊥AE,即AB⊥MN. 又CD∥AB,∴MN⊥CD. (3)由问(2)知,MN⊥CD,即AE⊥CD,再证AE⊥PD即可. ∵PA⊥平面ABCD,∴PA⊥AD. 又∠PDA=45°,E为PD的中点. ∴AE⊥PD,即MN⊥PD. 又MN⊥CD.∴MN⊥平面PCD. 【规律总结】 本题是涉及线面垂直、线面平行、线线垂直诸知识点的一道综合题.题(1)的关键是选取PD的中点E,所作的辅助线使问题处理方向明朗化.线线垂直←线面垂直←线线垂直是转化规律. |


科目:高中数学 来源: 题型:
 22、如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.
22、如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.查看答案和解析>>
科目:高中数学 来源: 题型:
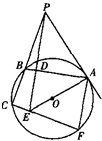 如图所示,已知PA切圆O于A,割线PBC交圆O于B、C,PD⊥AB于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF.
如图所示,已知PA切圆O于A,割线PBC交圆O于B、C,PD⊥AB于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF.| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
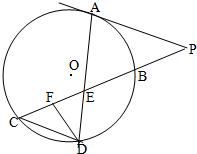 如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.
如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.查看答案和解析>>
科目:高中数学 来源: 题型:
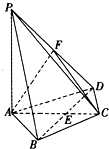 如图所示,已知PA⊥平面ABCD,PA=AB=AD=2,AC与BD交于E点,BD=2,BC=CD=
如图所示,已知PA⊥平面ABCD,PA=AB=AD=2,AC与BD交于E点,BD=2,BC=CD=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
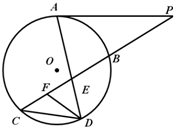 (2013•甘肃三模)选修4-1:几何证明选讲
(2013•甘肃三模)选修4-1:几何证明选讲查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com