
(Ⅰ)求椭圆C的方程;
(Ⅱ)若AB为垂直于x轴的动弦,直线l:x=4与x轴交于点N,直线AF与BN交于点M.
(ⅰ)求证:点M恒在椭圆C上;
(ⅱ)求△AMN面积的最大值.
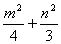
本小题主要考查直线与椭圆的位置关系、轨迹方程、不等式等基本知识,考查运算能力和综合解题能力,
解法一:
(Ⅰ)由题设a=2,c=1,从而b2=a2-c2=3,
所以椭圆C的方程为![]() .
.
(Ⅱ)(i)由题意得F(1,0),N(4,0).
设A(m,n),则B(m,-n)(n≠0),![]() =1. ……①
=1. ……①
AF与BN的方程分别为:n(x-1)-(m-1)y=0,
n(x-4)-(m-4)y=0.
![]() 设M(x0,y0),则有 n(x0-1)-(m-1)y0=0, ……②
设M(x0,y0),则有 n(x0-1)-(m-1)y0=0, ……②
n(x0-4)+(m-4)y0=0, ……③
由②,③得
x0=![]() .
.

所以点M恒在椭圆G上.
(ⅱ)设AM的方程为x=ty+1,代入![]() =1得(3t2+4)y2+6ty-9=0.
=1得(3t2+4)y2+6ty-9=0.
设A(x1,y1),M(x2,y2),则有:y1+y2=![]()
|y1-y2|=![]()
令3t2+4=λ(λ≥4),则
|y1-y2|=![]()
因为λ≥4,0<![]()
|y1-y2|有最大值3,此时AM过点F.
△AMN的面积S△AMN=![]()
解法二:
(Ⅰ)问解法一:
(Ⅱ)(ⅰ)由题意得F(1,0),N(4,0).
设A(m,n),则B(m,-n)(n≠0), ![]() ……①
……①
AF与BN的方程分别为:n(x-1)-(m-1)y=0, ……②
n(x-4)-(m-4)y=0, ……③
由②,③得:当x≠![]() . ……④
. ……④
由④代入①,得![]() =1(y≠0).
=1(y≠0).
当x=![]() 时,由②,③得:
时,由②,③得: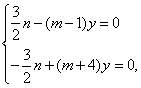
解得![]() 与a≠0矛盾.
与a≠0矛盾.
所以点M的轨迹方程为![]() 即点M恒在锥圆C上.
即点M恒在锥圆C上.
(Ⅱ)同解法一.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
(22) (本小题满分14分)
如图,椭圆![]() (a>b>0)的一个焦点为F(1,0),且过点(2,0).
(a>b>0)的一个焦点为F(1,0),且过点(2,0).
(Ⅰ)求椭圆C的方程;
(Ⅱ)若AB为垂直于x轴的动弦,直线l:x=4与x轴交于点N,直线AF与BN交于点M.
(ⅰ)求证:点M恒在椭圆C上;
(ⅱ)求△AMN面积的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
如图,椭圆![]() (a>b>0)的一个焦点为F(1,0),且过点(2,0).(Ⅰ)求椭圆C的方程;(Ⅱ)若AB为垂直于x轴的动弦,直线
(a>b>0)的一个焦点为F(1,0),且过点(2,0).(Ⅰ)求椭圆C的方程;(Ⅱ)若AB为垂直于x轴的动弦,直线![]() 与
与![]() 轴交于点N,直线AF与BN交于点
轴交于点N,直线AF与BN交于点![]() .求证:点M恒在椭圆C上.
.求证:点M恒在椭圆C上.
查看答案和解析>>
科目:高中数学 来源:2008年普通高等学校招生全国统一考试数学文史类(福建卷) 题型:解答题
(本小题满分14分)
如图,椭圆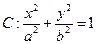 (a>b>0)的一个焦点为F(1,0),且过点(2,0).
(a>b>0)的一个焦点为F(1,0),且过点(2,0).
(Ⅰ)求椭圆C的方程;
(Ⅱ)若AB为垂直于x轴的动弦,直线l:x=4与x轴交于点N,直线AF与BN交于点M.
(ⅰ)求证:点M恒在椭圆C上;
(ⅱ)求△AMN面积的最大值.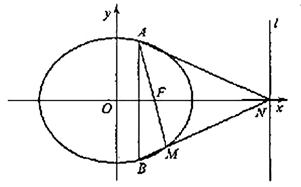
查看答案和解析>>
科目:高中数学 来源: 题型:

(Ⅰ)求椭圆的离心率;
(Ⅱ)若椭圆的长轴长等于4,Q是椭圆右准线l上异于点A的任意一点,A1、A2分别是椭圆的左、右顶点,直线QA1、QA2与椭圆的另一个交点分别为M、N,求证:直线MN与x轴交于定点.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省南京市宁海中学高二(上)期中数学试卷(解析版) 题型:解答题
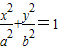 (a>b>0)过点
(a>b>0)过点 ,其左、右焦点分别为F1,F2,离心率
,其左、右焦点分别为F1,F2,离心率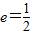 ,M,N是椭圆右准线上的两个动点,且
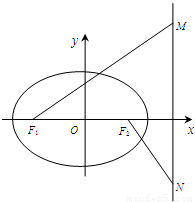
,M,N是椭圆右准线上的两个动点,且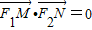 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com