Question

如果函数f(x)=ax⁵-bx³+c(a≠0)在x=±1时有极值,极大值为4,极小值为0,试求a,b,c的值.

Answer 1

思路分析:可通过求导确定可疑点,注意利用已知极值点x=±1所确定的相关等式,在判断y′的符号时,必须对a进行分类讨论.

解:y′=5ax⁴-3bx²,令y′=0,即5ax⁴-3bx²=0,x²(5ax²-3b)=0,

∵x=±1是极值点,

∴5a(±1)²-3b=0.

又x²＞0,∴可疑点为x=0,±1.

若a＞0,y′=5ax²(x²-1).

当x变化时,y′与y的变化情况如下表:

X	(-∞,1)	-1	(-1,0)	0	(0,1)	1	(1,+∞)
y′	+	0	-	0	-	0	+
Y	↗?	极大值	?↘	无极值	?↘	极小值	↗?

∴当x=-1时,f(x)有极大值;

当x=1时,f(x)有极小值.

∴

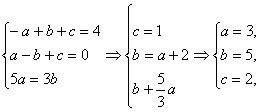
若a＜0,同理可得a=-3,b=-5,c=2.

    方法归纳 从逆向思维出发,运用待定系数法,实现由已知向未知的转化,转化过程中通过列表形象直观地解决待定系数问题.