练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图2-6-11,PA、PB分别切⊙O于A、B、C是上任意一点,过C作⊙O的切线DE分别交PA、PB于D、E,PO交AB于H,交⊙O于F,则下列结论:

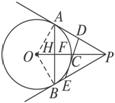
    ①△PDE周长是定值PA+PB;②AH2=OH·PH;③PA2=PO2-OF2;④PB2=PO·PH.

    其中正确的是(    )

    图2-6-11

    A.①②           B.①②③            C.②③④       D.①②③④

    解析:①由切线长定理,得DC=DA,EC=EB.

    ∴DE=AD+BE.

    ∴PD+DE+PE=PD+DA+BE+PE=PA+PB,正确.

    ②连结OA、OB,则P、A、O、B四点共圆,由相交弦定理,得

    AH·BH=OH·PH.

    ∵AH=BH,∴AH2=OH·PH.正确.

    ③延长PO交⊙O于G,由切割线定理,得PA2=PF·PG

    =(PO-OF)(PO+OG)

    =(PO-OF)(PO+OF)

    =PO2-OF2,正确.

    ④在Rt△POB中,BF⊥OP,由射影定理PB2=PO·PH,正确.

    答案:D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2012年江苏省高一上学期开学考试数学 题型：解答题

    （本题11分）如图，矩形ABCD中，AB=6，BC=2，点O是AB的中点，点P在AB的延长线上，且BP=3．一动点E从O点出发，以每秒1个单位长度的速度沿OA匀速运动，到达A点后，立即以原速度沿AO返回；另一动点F从P点出发，以每秒1个单位长度的速度沿射线PA匀速运动，点E、F同时出发，当两点相遇时停止运动，在点E、F的运动过程中，以EF为边作等边△EFG，使△EFG和矩形ABCD在射线PA的同侧．设运动的时间为t秒（t≥0）．

    （1）当等边△EFG的边FG恰好经过点C时，求运动时间t的值；

    （2）在整个运动过程中，设等边△EFG和矩形ABCD重叠部分的面积为S，求出S与t之间的函数关系式和相应的自变量t的取值范围；

     

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图2-3-11所示，已知点A(4,0),B(4,4),C(2,6),求AC和BD交点P的坐标.

    图2-3-11

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图2-5-11，已知⊙O1和⊙O2相交于点A、B，过点A作⊙O1的切线交⊙O2于点C，过点B作两圆的割线，分别交⊙O1、⊙O2于点D、E，DE与AC相交于点P.

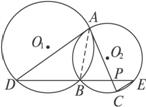
    图2-5-11

    （1）求证：AD∥EC；

    （2）若AD是⊙O2的切线，且PA=6，PC=2，BD=9，求AD的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知A(8,0)、B(0,6)和△AOB的内切圆：(x-2)2+(y-2)2=4,P(x,y)是圆上一点(如图所示)，

    (1)求P点到直线l:4x+3y+11=0距离的最大值和最小值;

    (2)若S=|PA|2+|PB|2+|PO|2，求S的最大值和最小值.

    查看答案和解析>>

    同步练习册答案