
过点P(2,1)的直线l交x轴、y轴正半轴于A、B两点,求使:
(1)△AOB面积最小时l的方程;
(2)|PA|·|PB|最小时l的方程.
(1)x+2y-4=0(2)x+y-3=0
方法一 设直线的方程为![]() (a>2,b>1),
(a>2,b>1),
由已知可得![]() . 2分
. 2分
(1)∵2![]() ≤
≤![]() =1,∴ab≥8. ∴S△AOB=
=1,∴ab≥8. ∴S△AOB=![]() ab≥4. 4分
ab≥4. 4分
当且仅当![]() =
=![]() =
=![]() ,即a=4,b=2时,S△AOB取最小值4,此时直线l的方程为
,即a=4,b=2时,S△AOB取最小值4,此时直线l的方程为![]() =1,即x+2y-4=0. 6分
=1,即x+2y-4=0. 6分
(2)由![]() +
+![]() =1,得ab-a-2b=0, 变形得(a-2)(b-1)=2,
=1,得ab-a-2b=0, 变形得(a-2)(b-1)=2,
|PA|·|PB|
=![]() ·
·![]()
=![]()
≥![]() . 10分
. 10分
当且仅当a-2=1,b-1=2,
即a=3,b=3时,|PA|·|PB|取最小值4.
此时直线l的方程为x+y-3=0. 12分
方法二 设直线l的方程为y-1=k(x-2) (k<0),
则l与x轴、y轴正半轴分别交于
A![]() 、B(0,1-2k).
、B(0,1-2k).
(1)S△AOB=![]()
![]() (1-2k)
(1-2k)
=![]() ×
×![]()
≥![]() (4+4)=4.
(4+4)=4.
当且仅当-4k=-![]() ,即k=-
,即k=-![]() 时取最小值,此时直线l的方程为y-1=-
时取最小值,此时直线l的方程为y-1=-![]() (x-2),即x+2y-4=0. 6分
(x-2),即x+2y-4=0. 6分
|
=![]() ≥4,
≥4,
当且仅当![]() =4k2,即k=-1时取得最小值,此时直线l的方程为y-1=-(x-2),即x+y-3=0. 12分
=4k2,即k=-1时取得最小值,此时直线l的方程为y-1=-(x-2),即x+y-3=0. 12分


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 椭圆E:
椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| AB |
| AN |
| BD |
| BN |
| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012届重庆市“名校联盟”高二第一次联考文科数学试卷(解析版) 题型:解答题
已知两条直线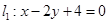 与
与 的交点为P,直
的交点为P,直
线 的方程为:
的方程为: .
.
(1)求过点P且与 平行的直线方程;
平行的直线方程;
(2)求过点P且与 垂直的直线方程.
垂直的直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com