
 …
… ≤1.
≤1. -1,当x>1时,f′(x)<0,当0<x<1时,f′(x)>0.
-1,当x>1时,f′(x)<0,当0<x<1时,f′(x)>0. -a=0,可得 x=
-a=0,可得 x= .
. 时,f′(x)<0,当0<x<
时,f′(x)<0,当0<x< 时,f′(x)>0. 故 f(x)在(0,
时,f′(x)>0. 故 f(x)在(0, )上是增函数,在(
)上是增函数,在( ,+∞)上是减函数.
,+∞)上是减函数. )=-lna-1.
)=-lna-1. 时,y=f(x)有2个零点;当a=
时,y=f(x)有2个零点;当a= 时,y=f(x)有1个零点; 当a>
时,y=f(x)有1个零点; 当a> 时,y=f(x)没有零点.
时,y=f(x)没有零点. 时,y=f(x)有1个零点; 当 0<a<
时,y=f(x)有1个零点; 当 0<a< 时,y=f(x)有2个零点; 当a>
时,y=f(x)有2个零点; 当a> 时,y=f(x)没有零点.
时,y=f(x)没有零点.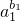 +ln
+ln 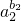 +…+ln
+…+ln 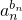 <a1b1+a2b2+…+anbn -( b1+b2+…+bn).
<a1b1+a2b2+…+anbn -( b1+b2+…+bn).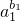 +ln
+ln 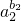 +…+ln
+…+ln 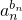 ≤0,即ln(
≤0,即ln(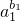 •
•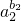 …
…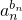 )≤0,
)≤0, …
… ≤1.
≤1. 时,y=f(x)有1个零点; 当 0<a<
时,y=f(x)有1个零点; 当 0<a< 时,y=f(x)有2个零点; 当a>
时,y=f(x)有2个零点; 当a> 时,y=f(x)没有零点.
时,y=f(x)没有零点.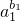 +ln
+ln 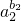 +…+ln
+…+ln 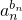 <a1b1+a2b2+…+anbn -( b1+b2+…+bn),再由已知条件证得
<a1b1+a2b2+…+anbn -( b1+b2+…+bn),再由已知条件证得  …
… ≤1成立.
≤1成立.

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2(x-1) |
| x+1 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| a |
| ||
| x |
| 6 |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com