解:(1)∵函数f(x)=lnx-x+1,x∈(0,+∞),∴f′(x)=
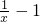
令其为0可得x=1,
并且当x∈(0,1)时,f′(x)>0,函数f(x)单调递增,
当x∈(1,+∞)时,f′(x)<0,函数f(x)单调递减,
故f(x)在x=1处取到极大值f(1)=0
(2)由(1)知,当x
1∈(0,1)时,f′(x)>0,函数f(x)单调递增,
故f(x
1)<f(1)=0,
因为a≥1,函数g(x)=x
2-3ax+2a
2-5,为开口向上的抛物线,对称轴为x=


故函数g(x)在区间(0,1)上为减函数,故g(1)<g(x
0)<g(0),
即g(x
0)<2a
2-5,
要使对于任意x
0∈(0,1),总存在x
1∈(0,1),使得f(x
1)=g(x
0)成立,
只需2a
2-5<0即可,解得

(3)由(1)可知f(x)在x=1处取到极大值f(1)=0,也是最大值,
故f(x)≤f(1)=0,即lnx-x+1≤0,即lnx≤x-1,当x=1时取等号,
可证

,又

,故

构造函数F(x)=

,则F′(x)=

=

>0
即函数F(x)在x∈(0,+∞)上单调递增,当x趋向于正无穷大时,F(x)趋向于0,
故F(x)<0,即

,
故有

分析:(1)求函数的导数,即可得到函数的单调区间和极值;
(2)分别求出两个函数的取值范围,要使对于任意x
0∈(0,1),总存在x
1∈(0,1),使得f(x
1)=g(x
0)成立,只需2a
2-5<0即可;
(3)结合(1)的结论可证后半部分,再利用构造函数的方式证明前半部分,可得答案.
点评:本题为函数导数的综合应用,构造函数通过导数来解决问题是关键,属中档题.

 .
.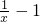 令其为0可得x=1,
令其为0可得x=1,


 ,又
,又 ,故
,故
 ,则F′(x)=
,则F′(x)= =
= >0
>0 ,
,


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案