
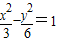 的右焦点F2,倾斜角为30°的直线交双曲线于A,B两点,O为坐标原点,F1为左焦点.
的右焦点F2,倾斜角为30°的直线交双曲线于A,B两点,O为坐标原点,F1为左焦点.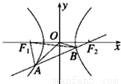 (1)解:由双曲线的方程得a=
(1)解:由双曲线的方程得a=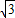 ,b=
,b=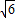 ,
,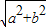 =3,F1(-3,0),F2(3,0).
=3,F1(-3,0),F2(3,0).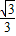 (x-3).
(x-3).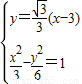 得5x2+6x-27=0.
得5x2+6x-27=0. ,x1x2=-
,x1x2=-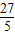 .
.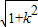 |x1-x2|=
|x1-x2|=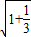 •
•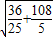 =
=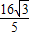
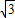 x-3y-3
x-3y-3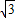 =0.
=0.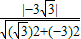 =
= .
. |AB|•d=
|AB|•d= ×
×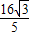 ×
× =
=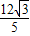 .…(8分)
.…(8分)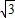 ,|BF1|-|BF2|=2
,|BF1|-|BF2|=2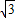 ,
,

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
(08年华师一附中二次压轴)过双曲线![]() 的右焦点F2的直线与右支交于A、B两点,且线段AF2、BF2的长度分别为m、n,m≥n.
的右焦点F2的直线与右支交于A、B两点,且线段AF2、BF2的长度分别为m、n,m≥n.
(Ⅰ)求证:mn≥1;
(Ⅱ)当直线AB的斜率k∈[![]() ,3]时,求
,3]时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省石家庄一中高二(上)第二次模拟数学试卷(解析版) 题型:选择题
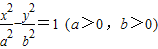 的右焦点F2作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为A,B.若
的右焦点F2作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为A,B.若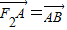 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省宜春市上高二中高二(下)第五次月考数学试卷(理科)(解析版) 题型:解答题
 的右焦点F2,作倾斜角为
的右焦点F2,作倾斜角为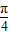 的直线交双曲线于A、B两点,
的直线交双曲线于A、B两点,查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省五校第二次联考数学试卷(文科)(解析版) 题型:选择题
 的右焦点F2作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为A,B.若
的右焦点F2作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为A,B.若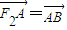 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )查看答案和解析>>
科目:高中数学 来源:高考数学一轮复习必备(第65课时):第八章 圆锥曲线方程-直线与圆锥曲线的位置关系(2)(解析版) 题型:选择题
 的右焦点F2作垂直于实轴的弦PQ,F1是左焦点,若∠PF1Q=90°,则双曲线的离心率是( )
的右焦点F2作垂直于实轴的弦PQ,F1是左焦点,若∠PF1Q=90°,则双曲线的离心率是( )


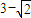
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com