已知函数f(x)=(-ax2-2x+a)•ex,(a∈R).
(1)当a=-2时,求函数f(x)的单调区间;
(2)若f(x)在[-1,1]上单调递减,求实数a的取值范围.
解:(1)a=-2时,f(x)=(2x
2-2x-2)•e
x,定义域为R.
f′(x)=)=(2x
2-2x-2)•e
x+(4x-2)•e
x=2(x-1)(x+2)•e
x.
由f′(x)>0得x<-2或x>1,由f′(x)<0,得-2<x<1,
∴f(x)的单调递增区间为(-∞,-2),(1,+∞),单调递减区间为(-2,-1).
(2)f′(x)=(-ax
2-2x+a)•e
x+(-2ax-2)•e
x=-[ax
2+2(a+1)x+2-a]•e
x.
令g(x)=-ax
2-2(a+1)x+a-2.
①当a=0时,g(x)=-2x-2,在(-1,1)内g(x)<0,f′(x)<0,
函数f(x)在[-1,1]上单调递减.
②当a>0时,g(x)=-ax
2-2(a+1)x+a-2是二次函数,其对称轴为x=-1-

<-1,
当且仅当g(-1)≤0,即a≤0时,f′(x)≤0,此时无解.
③当a<0时,g(x)=-ax
2-2(a+1)x+a-2是二次函数,
当且仅当
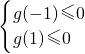
即

.∴-2≤a<0时,f′(x)≤0,
此时函数f(x)在[-1,1]上单调递减.
综上,实数a的取值范围是[-2,0].
分析:(1)把a=-2代入f(x),解不等式f′(x)>0,f′(x)<0即可;
(2)f(x)在[-1,1]上单调递减,即f′(x)≤0在[-1,1]上恒成立,对a进行分类讨论即可解出a的取值范围.
点评:本题考查导数与函数单调性的关系,对可导函数f(x)来说,f′(x)≤0(不总为0)是f(x)在某区间上单调递减的充要条件.

 <-1,
<-1,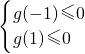 即
即 .∴-2≤a<0时,f′(x)≤0,
.∴-2≤a<0时,f′(x)≤0,

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案