
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
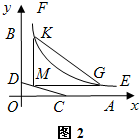
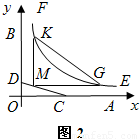
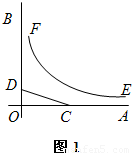
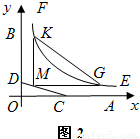
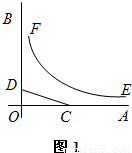
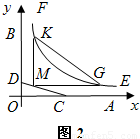
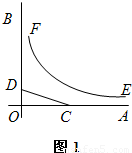
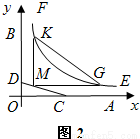
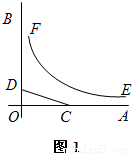
 如图1,OA,OB是某地一个湖泊的两条互相垂直的湖堤,线段CD和曲线段EF分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥CD上某点M分别修建与OA,OB平行的栈桥MG、MK,且以MG、MK为边建一个跨越水面的三角形观光平台MGK.建立如图2所示的直角坐标系,测得线段CD的方程是x+2y=20(0≤x≤20),曲线段EF的方程是xy=200(5≤x≤40),设点M的坐标为(s,t),记z=s•t.(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度
如图1,OA,OB是某地一个湖泊的两条互相垂直的湖堤,线段CD和曲线段EF分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥CD上某点M分别修建与OA,OB平行的栈桥MG、MK,且以MG、MK为边建一个跨越水面的三角形观光平台MGK.建立如图2所示的直角坐标系,测得线段CD的方程是x+2y=20(0≤x≤20),曲线段EF的方程是xy=200(5≤x≤40),设点M的坐标为(s,t),记z=s•t.(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南师大附中高三(下)第八次月考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2010-2011学年上海市浦东新区高三(下)期中数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:《三角函数》2013年高三一轮复习单元训练(北京师范大学附中)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2011年江苏省高考数学仿真押题试卷(05)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com