
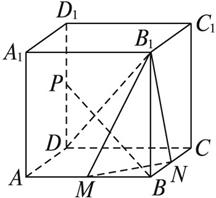
(1)若![]() ,求证:无论点P在DD1上如何移动,总有BP⊥MN.
,求证:无论点P在DD1上如何移动,总有BP⊥MN.
(2)若D1P∶PD=1∶2,且PB⊥平面B1MN,求二面角NB1MB的大小.
(3)在棱DD1上是否存在这样的点P,使得平面APC1⊥平面ACC1?证明你的结论.
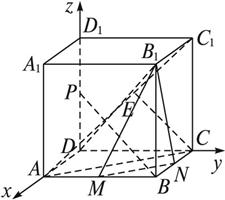
(1)证明:以DA、DC、DD1所在的直线分别为x、y、z轴建立空间直角坐标系,如右图所示.
设正方体棱长为1,则A(1,0,0),B(1,1,0),C(0,1,0),C1(0,1,1).
设M(1,1-x,0),N(1-x,1,0),P(0,0,z),则
![]() =(-x,x,0),
=(-x,x,0),![]() =(-1,-1,z).
=(-1,-1,z).
![]() =x-x=0,∴BP⊥MN.
=x-x=0,∴BP⊥MN.
(2)解:由条件知P(0,0,![]() ),
),![]() =(-1,-1,
=(-1,-1,![]() ),
),![]() =(-1,0,0),
=(-1,0,0),
![]() 、
、![]() 分别为面B1MN、面B1MB的法向量.
分别为面B1MN、面B1MB的法向量.
∴二面角N-B1M-B的大小等于〈![]() ,
,![]() 〉,
〉,
cos〈![]() ,
,![]() 〉=
〉=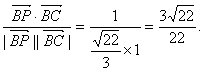
∴〈![]() ,
,![]() 〉=arccos
〉=arccos![]() .
.
所求二面角的大小为arccos![]() .
.
(3)解:不妨假设存在点P,则在平面ACC1内过C作CE⊥AC1,垂足为E.
设P(0,0,z),![]() =(-1,0,z),
=(-1,0,z),
![]() λ(-1,1,1),
λ(-1,1,1),
![]() =(-λ+1,λ-1,λ),
=(-λ+1,λ-1,λ),
由![]()
再由![]()
∴P为DD1中点,此时CE⊥AP.
故CE⊥平面APC1.
又CE![]() 平面ACC1,
平面ACC1,
∴平面APC1⊥平面ACC1.


 核心素养学练评系列答案
核心素养学练评系列答案科目:高中数学 来源: 题型:
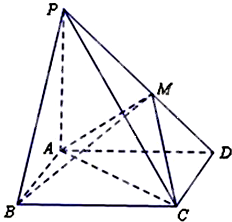 如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD,垂足为M.
如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD,垂足为M.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,点N在圆x2+y2=4上运动,DN⊥x轴,点M在DN的延长线上,且
如图所示,点N在圆x2+y2=4上运动,DN⊥x轴,点M在DN的延长线上,且| DM |
| DN |
| 1 |
| 2 |
| x |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,M,N分别是PA,BC的中点,且PD=AD=1.
如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,M,N分别是PA,BC的中点,且PD=AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:
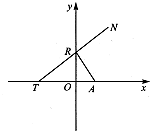 如图所示,点A(p,o)(p>0),点R在y轴上运动,点T在x轴上,N为动点,且
如图所示,点A(p,o)(p>0),点R在y轴上运动,点T在x轴上,N为动点,且| RT |
| RA |
| RN |
| RT |
| PM |
| QM |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com