在△ABC中,a=3,b=2,A=60°,求cosB及c的值.
【答案】
分析:直接利用正弦定理求出B的正弦值,利用同角三角函数的基本关系式求出B的余弦值,通过余弦定理求出c的大小.
解答:解:因为△ABC中,a=3,b=2,A=60°,
由正弦定理可知sinB=
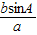
=
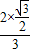
=
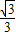
,因为a>b,B=60°.所以cosB=
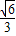
.
由余弦定理可知:c
2=a
2+b
2-2abcosC
=a
2+b
2-2abcos(π-A-B)
=a
2+b
2+2abcos(A+B)
=13+12cosAcosB-12sinAsinB
=13+12×
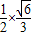
-12×
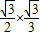
=7+2
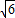
,
∴
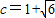
.
点评:本题考查正弦定理与余弦定理的应用,三角形的解法,考查计算能力.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案