Question

计算cos(+α)+cos(+α)+cosα.

Answer 1

分析：构造三个向量a=(sinα,cosα),b=(sin(π+α),cos(π+α)),c=(sin(π+α),cos(π+α)),利用a,b,c之间的关系求解.

解:令a=(sinα,cosα),b=(sin(π+α),cos(π+α)),

c=(sin(π+α),cos(π+α)).

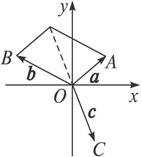
如图所示,|a|=|b|=|c|=1,cos∠AOB==sinαsin(π+α)+cosαcos(π+

α)=cosπ,同理,cos∠BOC=cos∠COA=cosπ.由向量加法的几何意义得a+b=-c.所以a+b+c=0,

即cosα+cos（+α）+cos(+α)=0.

点评：本题的计算利用了平面向量的数量积、向量加法的平行四边形法则，体现了数形结合的思想.