
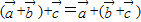
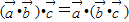 ;
;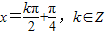 .
.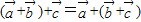 ,故①是真命题;
,故①是真命题;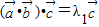 是与
是与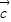 共线的一个向量,
共线的一个向量,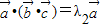 是与
是与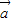 共线的一个向量,所以
共线的一个向量,所以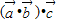 与
与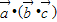 不一定相等,故②是假命题;
不一定相等,故②是假命题;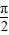 +kπ或m=kπ,k∈Z}
+kπ或m=kπ,k∈Z} kπ,0),而不是(kπ,0),故③为假命题;
kπ,0),而不是(kπ,0),故③为假命题;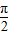 +kπ,k∈Z,得
+kπ,k∈Z,得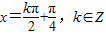 ,
,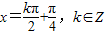 ,得④是真命题.
,得④是真命题.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AB |
| AC |
| BC |
| AC |
| AB |
| OP |
| 0A |
| AB |
| AC |
| OA |
| OC |
| OB |
| 0 |
| S△AOC |
| S△ABC |
| 1 |
| 3 |
| ||
丨
|
| ||
丨
|
| BC |
| ||
丨
|
| ||
丨
|
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
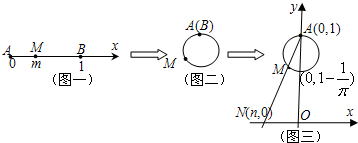 如图揭示了一个由区间(0,1)到实数集R上的对应过程:区间(0,1)内的任意实数m与数轴上的线段AB(不包括端点)上的点M一一对应(图一),将线段AB围成一个圆,使两端A,B恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1)(图三).图三中直线AM与x轴交于点N(n,0),由此得到一个函数n=f(m),则下列命题中正确的序号是( )
如图揭示了一个由区间(0,1)到实数集R上的对应过程:区间(0,1)内的任意实数m与数轴上的线段AB(不包括端点)上的点M一一对应(图一),将线段AB围成一个圆,使两端A,B恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1)(图三).图三中直线AM与x轴交于点N(n,0),由此得到一个函数n=f(m),则下列命题中正确的序号是( )| 1 |
| 2 |
| 1 |
| 2 |
| A、(1)(3)(4) |
| B、(1)(2)(3) |
| C、(1)(2)(4) |
| D、(1)(2)(3)(4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com